cnd do poduszki na na dzień dobry
Saizou : x4+9=(x2+3)2−(√6x)2=(x2+3−√6x)(x2+3+√6x)
25 lip 18:16
Eta:


25 lip 18:22
Saizou : to teraz pogłówkuję nad zadaniem Ety o dzielnikach naturalnych liczby 11! , a ostatni
przykład zrobię w niedalekiej przyszłości
25 lip 18:35
Eta:
A już myślałam,że zignorowałeś to zadanko

25 lip 18:36
Saizou : 11!=11*10*9*8*7*6*5*4*3*2*1
liczba ilość dzielników
1 1
2 2
3 2
4 3
5 2
6 4
7 2
8 4
9 3
10 4
11 2
z reguły mnożenia mamy 1*2
5*3
2*4
3=18 432

25 lip 18:42
Eta:
Nieco za mało

25 lip 18:52
Saizou : wracając do wielomianu
x8+x4+1=(x4+1)2−x4 = (x4+1−x2)(x4+1+x2)=(x4−x2+1)(x4+x2+1)=
((x2+1)2−3x2)((x2+1)2−x2)=(x2+1−√3x)(x2+1+√3x)(x2+1−x)(x2+1+x)
25 lip 18:55
Saizou : jakaś odpowiedź?
25 lip 19:10
Mila: Wielomian − Wynik dobry.
No to te dzielniki licz.
25 lip 19:14
Saizou : czy to będzie 540

25 lip 19:18
Artur z miasta Neptuna:
a czy to nie będzie tak ...

11! = 11*10*9*8*7*6*5*4*3*2 = 2
8*3
4*5
2*7
1*11
1
a więc dzielnik liczby 11! musi być postaci: 2
a3
b5
c7
d11
e
gdzie:
a= 0,1,2,3,4,5,6,7,8
b= 0,1,2,3,4
c= 0,1,2
d= 0,1
e= 0,1
ile różnych takich zestawów możesz zrobić

Tyle że wtedy liczb dzielników będzie o wiele wiele wiele mniejsza niż sugerowana przez Etę.
25 lip 19:18
Eta:
Odp:
540 dzielników

25 lip 19:31
Saizou : 11!=28*34*52*7*11
(8+1)(4+1)(2+1)(1+1)(1+1)=9*5*3*2*2=540
25 lip 19:36
Eta:


25 lip 19:37
Saizou : to teraz zadanie do kolacji

25 lip 19:38
Eta:
Nie jadam o tej porze kolacji

25 lip 19:39
Saizou : to zadanie na wczesny letni wieczór

25 lip 19:40
Eta:
6/ Oblicz, bez użycia tablic wartość
| | sin40o*sin50o | |
|
| = .......... |
| | 5sin100o | |
25 lip 19:41
Eta:
7/ Wykaż, że liczba : 2log35− 5log32 jest parzysta
25 lip 19:43
Saizou : Eto i tu Cię zmartwię że nasza nauczycielka stwierdziła że trygonometrię mamy w drugiej
klasie. ja znam tylko definicje funkcji trygonometrycznych kąta ostrego

25 lip 19:43
Saizou : mogę Ci powiedzieć że korzystałem z podręcznika Matematyka z Plusem wydawnictwa GWO
25 lip 19:45
Eta:
Hmmm

Myślałam, że jesteś przyszłorocznym maturzystą z rozszerzeniem

25 lip 19:45
Saizou : to musiał Ci się coś pokręcić

gdzie z taką niewiedzą
25 lip 19:46
Eta:
8/ Wyznacz wszystkie liczby pierwsze spełniające równanie:
xy−y= x+5
25 lip 19:50
Eta:
Sorry

teraz zauważyłam,że napisałeś
1 LO rozszerzony 
25 lip 19:53
Mila: To może z Nowika:
Dla jakich wartości parametru k rozwiązaniem układu
x+2y=1
2x+y=k jest para liczb dodatnich?
25 lip 19:58
Eta:
| | n4 | | n3 | | n2 | |
9/ Wykaż,że liczba : |
| + |
| + |
| |
| | 4 | | 2 | | 4 | |
jest kwadratem liczby całkowitej
10/ Wykaż,że dla n€N
liczba : (n−2)
4−n
4 jest podzielna przez 8
Wystarczy ? .... na tę kolację, czy " zjesz " więcej?

25 lip 20:02
Saizou : | | x+5 | |
mam pytanie czy zadanie od Ety można zrobić opierając się o wykres funkcji y= |
| i |
| | x−1 | |
odczytać, że x=2, a y=7

25 lip 20:03
Saizou : zadanie 9 niedawno robiłem, parametr zostawię na deser

a teraz wezmę się za 10
25 lip 20:04
Saizou : (n−2)4−n4=8t , t ∊C
(n−2)2(n−2)2−n4
(n2−4n+4)(n2−4n+4)−n4=n4−4n3+4n2−4n3+16n2−16n+4n2−16n+16−n4=
−8n3+24n2−32n+16=8*(n3+3n2−4n+2)=8t, bo (n3+3n2−4n+2)∊C
25 lip 20:13
Saizou : zadanie 9
| n4 | | n3 | | n2 | | n4 | | 2n3 | | n2 | | n2(n2+2n+1) | |
| + |
| + |
| = |
| + |
| + |
| = |
| =
|
| 4 | | 2 | | 4 | | 4 | | 4 | | 4 | | 4 | |
25 lip 20:17
Saizou : 2x+y=k→y=−2x+k
| | 1 | | 1 | |
miejscem zerowym funkcji y=− |
| x+ |
| jest x=1 i jest to funkcja malejąca
|
| | 2 | | 2 | |
funkcja y=−2x+k jest również malejąca, a parametr k jest odpowiedzialny za miejsce zerowe tej
funkcji i punkt przecięcia z osią Y, zatem funkcja y=−2x+k musi mieć miejsce zerowe niż 1,
wówczas
0>−2*1+k→k<2, zatem k∊(2:+∞)
25 lip 20:40
Eta:
Nieco więcej takich liczb

Zad.8 x=2 i y=7 v x=7 i y=2 v x=3 i y=4 v x=4 i y=3
25 lip 21:36
Saizou : miały być liczby pierwsze zatem dwie ostatnie pary odpadają
25 lip 22:23
Mila: Saizou, rozwiąż a nie filozofuj. Błędna odpowiedź do układu.
Wyznacz x i y w zależności od parametru.
25 lip 22:43
Saizou : Mila a możesz podać odpowiedź?
25 lip 23:12
Eta:
No tak

( nie przeczytałam ... pomyślałam o naturalnych

25 lip 23:15
Mila: | | 1 | |
k należy do przedziału ( |
| ,2) |
| | 2 | |
26 lip 00:01
nikt : x+2y=1
2x+y=k
Szukamy k dla którego x oraz y będą dodatnie

W = −3
W
x = 1 − 2k
W
y = k − 2
| | Wx | | 1 − 2k | | 1 | |
x = |
| = |
| > 0 ⇒ 1 − 2k < 0 ⇒ 1 < 2k ⇒ k > |
| |
| | W | | −3 | | 2 | |
| | Wy | | k−2 | |
y = |
| = |
| > 0 ⇒ k−2 < 0 ⇒ k < 2 |
| | W | | −3 | |
| | 1 | |
Szukamy iloczynu tych rozwiązań więc : k ∊ ( |
| ; 2 ) |
| | 2 | |
26 lip 03:37
nikt : | sin40o * sin50o | | 2cos50o sin50o | | 1 | |
| = |
| = |
| |
| 5sin100o | | 10 sin100o | | 10 | |
26 lip 03:42
nikt : 2
log3 5 −5
log3 2 = ?
Najpierw wykażemy że te dwie liczby są równe czyli :
2
log3 5 = 5
log3 2
log
2 2{
log
3 5} = log
2 5{
log
3 2}
log
3 5 = log
2 5 * log
3 2 // log
3 2
| log3 5 | |
| = log2 5 korzystamy z twierdzenia o zmianie podstawy logartmu i mamy że : |
| log3 2 | |
log
2 5 = log
2 5 więc :
2
log3 5 = 5
log3 2 a z tego wynika że
2
log3 5 −5
log3 2 = 5
log3 2 −5
log3 2= 0 ∊ parzystych
26 lip 03:46
Saizou : na pomysł z wyznacznikami wpadłem jak wyłączyłem komputer

26 lip 13:31
nikt : Wrzucę jakieś zadanko może ktoś się skusi
 Zad
Zad :
W kąt o mierze 60
o wpisano koło, a następnie dopisano jeszcze cztery koła tak, że każde
następne jest styczne zewnętrznie do poprzedniego i do ramion kąta.
a)uzasadnij, że długości promieni tych kół tworzą ciąg geometryczny.
b)oblicz, ile razy suma pól wszystkich pięciu kół jest większa od pola najmniejszego koła.
26 lip 13:57
Mila: ICSP − zadanie było dla Saizou, można też bez wyznaczników.

26 lip 14:32
nikt : hmmm no to teraz
Saizou zrobi bez wyznaczników

26 lip 14:36
Saizou : + rysunek
http://img19.imageshack.us/img19/1196/wykresyr.jpg
| | 1 | | 1 | |
funkcja m:y=− |
| x+ |
| ma miejsce zerowe równe x=1 i przecina oś Y w punkcie |
| | 2 | | 2 | |
| | 1 | |
P=(0: |
| ), z tego wynika, że funkcja l:y=−2x+k musi przecinać wykres funkcji m w tym |
| | 2 | |
fragmencie zaznaczonym na zielono. Zatem będę szukać parametru k dla którego funkcja l ma
| | 1 | |
miejsce zerowe mniejsze niż 1 i musi przecinać OŚ Y w punkcie większym niż G=(0: |
| ), |
| | 2 | |
wówczas
| | 1 | |
wiadomo,że parametr k odpowiada za przecięcie się wykresy z osią Y zatem k> |
| oraz
|
| | 2 | |
0=−2x+k→2x=k było by to miejsce zerowe, a wiem że ma być ono mniejsze niż 1 więc mogę zapisać,
| | 1 | |
że 2*1<k→2<k zatem odpowiedź to k∊( |
| :2) |
| | 2 | |
26 lip 16:48
Saizou : nie maiłem jeszcze ciągów, ale myślę że to będzie się opierać o podobieństwo trójkątów, albo o
tw.Talesa
26 lip 17:26
nikt : Ja to zrobiłem z podobieństwa

26 lip 17:29
Mila: wyznaczam x i y w zależności od k
x+2y=1 /(−2)
2x+y=k
−2x−2y=−2
2x+y=k dodaję stronami
y=2−k
x+2y=1
2x+y=k /(−2)
x+2y=1
−4x−2y=−2k dodaję stronami
rozwiązuję układ nierówności: x>0 i y>0
2−k>0
26 lip 17:40
Saizou : to może jeszcze jedno zadanie? bo się nudzę
26 lip 17:41
Saizou : ja to opisowo zrobiłem

26 lip 17:41
Saizou : tylko nie parametry
26 lip 17:42
Mila: Saizou zrób zadanie 8, algebraicznie, nie metodą prób i błędów.To jest ważne zadanie.
26 lip 17:42
nikt : rozwiąż równanie :
x3 + 3x2 + 3x + 10 = 0
26 lip 17:42
Saizou : co do zadania Ety ponowionego przez Milę to:
xy−y=x+5
−y(−x+1)+(−x+1)=6
(−x+1)(−y+1)=6 liczbę 6 można przedstawić za pomocą liczb całkowitych na 8 sposobów
1)
−x+1=6→x=−5
−y+1=1→y=0 sprzeczność z warunkami zadania
2)
−x+1=1→x=0
−y+1=6→y=−5 sprzeczność
3)
−x+1=3→x=−2
−y+1=2→y=−1 sprzeczność
4)
−x+1=2→x=−1
−y+1=3→y=−2 sprzeczność
5)
−x+1=−6→x=7
−y+1=−1→y=2 zatem OK
6)
−x+1=−1→x=2
−y+1=−6→y=7 zatem OK
7)
−x+1=−3→x=4
−y+1=−2→y=3 sprzeczność
8)
−x+1=−2→x=3
−y+1=−3→y=4 sprzeczność, wiec są tylko dwie pary liczb spełniających to równanie:
x=7 i x=2
y=2 y=7
26 lip 18:16
Saizou : x3+3x2+3x+10=(x+1)3+(3√32)3 i zastanawiam się co dalej
26 lip 18:30
Basia:
wskazówka:
a3+b3 = (a+b)(a2−ab+b2)
26 lip 18:32
Saizou : [(x+1)+3√32][(x+1)2−(x+1)3√32+(3√32)2]=0
[(x+1)+3√32]=0 lub [(x+1)2−(x+1)3√32+(3√32)2]=0
x=−1−3√32 bo z drugiego nie ma pierwiastka
26 lip 18:43
Basia: 
26 lip 18:46
Saizou : jakieś jeszcze? a wy z tymi wielomianami wykończycie

26 lip 18:57
nikt : masz to moje jeszcze

26 lip 19:00
Basia: które ? bo się pogubiłam........
26 lip 19:00
Saizou : ale już mówiłem że nie miałem ciągów
26 lip 19:01
nikt : wolisz wielomiany czy ciągi?
26 lip 19:02
nikt : Basiu moje z godziny 13:57
26 lip 19:02
Saizou : może coś jeszcze innego

26 lip 19:04
Basia: pytanie było do wpisu Saizou z 18:57
26 lip 19:04
nikt : Udowodnij że n5 − n jest podzielne przez 5
26 lip 19:05
Saizou : chodzi o zadania na poziomie 1 LO rozszerzenie
26 lip 19:06
Basia: to znaczy, że to jest za łatwe ?

26 lip 19:07
Basia:
Zaznacz na płaszczyźnie zbiór punktów, których współrzędne spełniają układy nierówności:
1.
y ≥ |x| − 2
i
|y|≤1
2.
|x−y| ≤ 2
i
y > 2
Rozwiązanie ma obejmować sposób w jaki dochodzisz do rysunku.
26 lip 19:12
Saizou : Basiu nie jest za łatwe

26 lip 19:12
pigor: 7/ Wykaż, że liczba : 2
log35− 5
log32 jest parzysta ..
no to może jeszcze np. tak :
niech
2log35=x i
5log32=y i na pewno x,y>0 (dlaczego?) ⇒
log
32
log35= log
3x i log
35
log32= log
3y ⇔
⇔ log
35 log
32= log
3x i log
32 log
35= log
3y ⇒
log3x=log3y ⇒
x=y ⇔
⇔
x−y=0 − jest
liczbą parzystą . ...

26 lip 19:14
Saizou : n5−1=5t t∊C
n(n4−1)=n(n2−1)(n2+1)=n(n−1)(n+1)(n2+1)=(n−1)n(n+1)[(n+1)2−(√2n)2]=
(n−1)n(n+1)[(n+1)−√2n)][(n+1)+√2n]
i co dalej?
26 lip 19:18
Basia:
no to przecież ono polega na rozkładzie n5 − n na czynniki i wyciągnięciu wniosków
próbuj; naprawdę nie jest bardzo trudne
26 lip 19:18
Basia:
W(n)=(n−1)*n*(n+1)(n2+1)
i teraz przypadki:
1.
5|n ⇒ oczywiste
2.
n = 5k+1 ⇒
w(n) = 5k*(5k+1)*(5k+2)*(25k2+10k+1) i już oczywiste
3.
n = 5k+2 ⇒
n−1 = 5k+1
n+1 = 5k+3
n2+1 = 25k2+10k+4+1 = 5(5k2+2k+1)
4.
n = 5k+3
5.
n = 5k+4
rozważasz tak samo
26 lip 19:24
pigor: ... i 8/ Wyznacz wszystkie liczby pierwsze spełniające równanie
: xy−y= x+5 ,
np. tak : a więc szukam par
(x,y)=? − liczb
pierwszych x≥2 i y≥ takich,
że
xy−y= x+5 ⇔ y(x−1}= x+5 /:(x−1) >0 ⇔ y=
x+5x−1 ⇔ y=
x−1+6x−1 ⇔
⇔
y=1+6x−1 , gdzie
x∊{2,3,5,7} ⇒ tylko pary
(2,7), (7,2) spełniają
warunki zadania . ...

26 lip 19:25
Saizou : Basiu no to teraz to już jest oczywiste, tylko jak na to wpaść

26 lip 19:27
Basia:
pierwsza zasada: pytają o podzielność ⇒ myślimy o resztach z dzielenia
powinieneś Saizou kupić sobie jakiś zbiór zadań do rozszerzenia i systematycznie
rozwiązywać;
najlepiej na razie po kolei
po jakimś czasie "z automatu" będziesz wiedział co i kiedy zastosować
polecam zbiory maturalne Kiełbasy, one wcale nie są takie typowo maturalne
doskonale dają się zastosować do bieżącej pracy w szkole,
bo układ treści pokrywa się z układem materiału
26 lip 19:33
nikt : n2+1 = n2 − 4 + 5 = (n−2)(n+2) + 5
i dalej korzystając z postu Basi mamy że:
(n−1)n(n+1)[(n−2)(n+2) + 5] = (n−2)(n−1)n(n+1)(n+2) + 5(n−1)n(n+1) co oczywiście dzieli się
przez 5
26 lip 19:34
Saizou : pomyślimy nad zakupem
26 lip 19:39
Saizou : właśnie pobrałem 4 pierwsze rozdziały
26 lip 19:58
Saizou : to co 2 zadanka na dobranoc

26 lip 23:09
Basia: napisałam Ci; o 19:12
26 lip 23:09
nikt: i masz jeszcze moje z 13:57
26 lip 23:10
Saizou : Basiu przeprasza, nie zauważyłem, a mówiłem że ciągów nie omawiałem
26 lip 23:12
nikt: wielomianów też xD
26 lip 23:13
Saizou : wielomiany tak na własną rękę

26 lip 23:14
nikt: to spróbuj tak z ciągami

W tym zadaniu są same podstawy ciągów.
26 lip 23:20
Saizou :
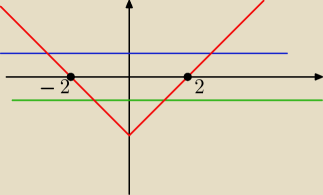
y≥lxl−2 i lyl≤1
y≤1 i y≥−1 i teraz narysuję sobie funkcje y=−1 i y=1 oraz funkcję y=lxl i przesunę ją o 2
jednostki w dół, zatem y∊<−1:1> ,a x∊<−3:−1>∪<1:3>
26 lip 23:25
Basia:
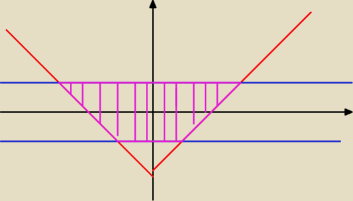
nie do końca dobrze to jest
proste i wykres w porządku
teraz
−1 ≤ y ≤ 1
to pas między prostymi (razem z nimi)
a
y ≥ |x|−2
to to czerwony wykres plus to co powyżej niego
fioletowe to część wspólna czyli rozwiązanie układu
26 lip 23:32
Saizou : a czy można zapisać lx−yl=lxl−lyl

26 lip 23:36
Basia:
|2−5| = |−3| = 3
|2| − |5| = 2−5 = −3
to można czy nie ?
tutaj musisz rozważyć dwa przypadki:
1. x−y≥0
2. x−y<0
26 lip 23:39
Saizou :
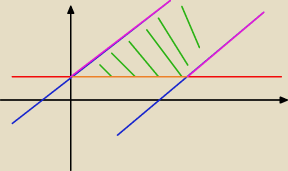
czyli rysuję prostą y=2 oraz funkcje y=x−2 i y=x+2 czyli rozwiązanie to obszar zielony z
różowymi liniami, ale bez pomarańczowej

26 lip 23:46
Saizou : znaczy się to jest źle rysuję juz inną wersję
26 lip 23:52
Saizou :
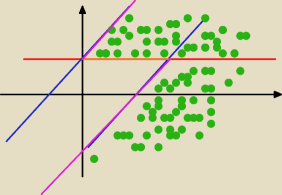
26 lip 23:56
Basia:
ależ poprzednie było dobrze

zaraz policzymy spokojnie
26 lip 23:59
Basia:
1.
x−y≥0 ⇔ y≤x
wtedy mamy
x−y ≤ 2
y ≥ x − 2
2.
x−y < 0 ⇔ y>x
wtedy mamy
−x+y ≤ 2
y ≤ x+2
czyli
[ y≤x ∧ y≥ x−2 ] ∨ [ y>x ∧ y≤x+2 ] ⇔
[ y≤x ∨ y>x ] ∧ [ y≤x ∨ y≤x+2 ] ∧ [ y≥ x−2 ∨ y>x] ∧ [ y≥x−2 ∨ y ≤ x+2 ] ⇔
cała płaszczyzna ∧ y≤ x+2 ∧ y≥x−2 ∧ cała płaszczyzna ⇔
y ≥ x−2 ∧ y≤ x+2
czyli to jest pas między tymi prostymi razem z nimi
czyli jest tak jak narysowałeś na pierwszym rysunku
27 lip 00:09
Saizou : i już chyba wiem dlaczego ten pierwszy jest dobrze
bo mamy z warunków y>2
a potem mamy, że y≥x+2 lub y≤x−2
y≥x+2 ta nierówność spełnia założenia że y>2
a dla y≤x−2 nie jest spełnione założenie y>2
dlatego zostaje tylko ten fragment między funkcjami i prostą y=2
27 lip 00:11
Saizou : to mogę prosić o ostatnie zadanie, takie na 'dobranoc'
27 lip 00:14
Basia:
to rozwiązanie, które Ci napisałam opiera się na logice i rachunku zdań, ale można też inaczej
rysujesz (1) czyli
y≤x i y≥x−2
pas między prostymi y=x i y=x−2
rysujesz (2) czyli
y≥x i y≤ x+2
pas między prostymi y=x i y=x+2
sumujesz to czyli masz pas między prostymi: y = x−2 y=x+2
rysujesz y=2 i bierzesz to co powyżej niej
27 lip 00:17
Eta:
Na dobranoc
łatwiutkie 
Która z liczb jest większa: 2
791 czy 5
339
27 lip 00:21
Basia:
Dla jakich wartości parametrów m,n
W(x) = 2x3 + mx2 − 13x + n
jest podzielny przez P(x) = x2 − 5x + 6
27 lip 00:22
Saizou : (27)113 (53)113
128113 > 125113
27 lip 00:24
Eta:


27 lip 00:29
Basia: moje też łatwiutkie

27 lip 00:30
Eta:
No też,też

27 lip 00:30
nikt: Eta a to co ja wrzuciłem

27 lip 00:31
Eta:
Nikt ..... jak Twój nick


27 lip 00:33
Saizou : to parametry zostawiam na jutro na śniadanie ok 11

a teraz wszystkim życzę miłej nocy
27 lip 00:34
Basia: Eto zlituj się; jeszcze nie daj boże
Saizou uwierzy

27 lip 00:34
Eta:
Miłych snów

27 lip 00:34
Saizou : Hornerem dzieli się przez wielomian x−a
27 lip 00:34
nikt: Nikt − to określenie pasuje do mnie idealnie

27 lip 00:35
Saizou : i dla każdego

za poświęcony czas
27 lip 00:35
nikt: wolę


27 lip 00:35
Eta:
A jednak
Saizou nie uwierzył

i za to

27 lip 00:38
Basia:
@nikt
Saizou najwyraźniej nie chce jeszcze zajmować się ciągami.
Z podobieństwa to powinno łatwo dać się policzyć, jeszcze z takim ułatwieniem: α=60
Jakbyś nic o ciągach nie pisał tylko polecił policzyć promień np.trzeciego w zależności od
pierwszego pewnie by się za to wziął.
27 lip 00:38
Eta:
A Ty co? nikt nie chce Cię utulić ?

27 lip 00:39
Saizou : to specjalnie dla
Nikt 
swoją drogą zaimek nikt się nie odmienia
27 lip 00:39
Saizou : ale tak sobie myślę że to zadanie o ciągu może zrobię
27 lip 00:40
nikt: Basiu
Ja go chciałem po prostu zachęcić do poczytania troszkę o ciągach

Według mnie są najłatwiejszym materiałem przerabianym w II klasie liceum

27 lip 00:41
Basia:
Nikt = Odyseusz = Ulisses
możesz go tak tytułować np. Odysku kochany...............

27 lip 00:41
27 lip 00:42
Saizou : P(x)=x
2−5x+6=(x−3)(x−2)
zatem
W(3)=2*3
3+m3
2−13*3+n=9m+15+n
W(2)=2*2
3+m2
2−13*2+n=4m+n−10
9m+n=−15
−4m−n=−10
=========
5m=−25
m=−5
n=10−4*(−5)=30
27 lip 10:47
Saizou : http://img853.imageshack.us/img853/1568/cigj.jpg
a)
2l=2r+r+l→l=3r
2k=2r+r+3r+3r+5→k=9r
2m=2r+r+3r+3r+9r+9r+m→m=27r
2n=2r+r+3r+3r+9r+9r+27r+27r+n→n=81r
zatem dla dowolnego promienia zachodzi
r
n=3r
n−1, zatem jest to ciąg geometryczny o q=3
b) p
k=πr
2
p
1=r
2π
p
2=9r
2π
p
3=81r
2π
p
4=729r
2π
p
5=6561r
2π
===========
p
c=7381r
2π
| 7381r2π | |
| =7381 razy większa |
| 1r2π | |
27 lip 13:17
nikt: wynik dobry

Jak widać zadanko nie było takie trudne

27 lip 13:21
nikt: Kolejne zadanko:
Reszta z dzielenia wielomianu x
3 + px
2 −x +q przez trójmian (x+2)
2 wynosi 1 − x.
Wyznacz pierwiastki tego wielomianu.
Jednak to chciałbym abyś rozwiązał
Dwoma sposobami

27 lip 13:23
Saizou : tylko trzeba było poczytać troszkę o ciągach

to co może jeszcze jedno zadanie

np. na dowód

27 lip 13:23
Saizou : a tam nie powinno być −x
3
27 lip 13:29
nikt: nie.
27 lip 13:30
Saizou : albo reszta nie powinna być (1
+x)

27 lip 13:32
nikt: nie.
27 lip 13:32
Saizou : tylko, że jak pomnożymy (x+2)2(1−x)=−x3−3x2+4
27 lip 13:34
nikt: od kiedy reszta jest trzecim pierwiastkiem wielomianu ?
27 lip 13:35
Saizou : od dzisiaj

tworzę nową matematykę

27 lip 13:36
Saizou : (x
2+4x+4)(ax+b)+1−x=x
3+px
2−x+q
ax
3+4ax
2+4ax+bx
2+4bx+4b+1−x=x
3+px
2−x+q
ax
3+(4a+b)x
2+(4a+4b)x+4b+1−x=x
3+px
2−x+q
zatem
| ⎧ | a=1 | |
| ⎜ | 4a+b=p | |
| ⎨ | 4a+4b=−1 |
|
| ⎩ | 4b+1−x=q | |
i pytanie czy dobrze liczę

27 lip 14:02
Saizou : poprawka bo
ax
3+(4a+b)x
2+(4a+4b−1)x+4b+1
| ⎧ | a=1 74a+b=p | |
| ⎨ | 4a+4b−1=−1 |
|
| ⎩ | 4b+1=q | |
27 lip 14:06
Saizou : zatem a=1
4+4b=0→b=−1
−4+1=q→q=−3
4−1=p→p=3
27 lip 14:11
Saizou : i wstawiając to do wielomianu
x3+3x2−x−3=0
x3−x+3x2−3=0
x(x2−1)+3(x2−1)=0
(x2−1)(x+3)=0
(x−1)(x+1)(x+3)=0
x=1 x=−1 x=−3
27 lip 14:15
rumpek: Wielomian W(x) = x
4 + ax
3 + bx
2 − 24x + 9 jest kwadratem wielomianu P(x) = x
2 + cx + d.
Oblicz a i b.

Takie proste zadanko z matury.
27 lip 14:16
nikt: wynik

pierwiastki

27 lip 14:21
Saizou : W(x)=(P(x))
2
(x
2+cx+d)(x
2+cx+d)=x
4+cx
3+dx
2+cx
3+c
2x
2+cdx+dx
2+cdx+d
2=x
4+2cx
3+(2d+c
2)x
2+2cdx+d
2
x
4+2cx
3+(2d+c
2)x
2+2cdx+d
2=x
4+ax
3+bx
2−24x+9
przyrównując odpowiednie współczynniki otrzymujemy
| ⎧ | 2c=a | |
| ⎜ | 2d+c2=b | |
| ⎨ | 2cd=−24 |
|
| ⎩ | d2=9 | |
zatem będą dwie możliwości
1)
d=3
c=−4
b=0
a=−8
2)
d=−3
c=4
b=32
a=8
27 lip 14:46
rumpek: Zadanie pyta o a i b, a masz dobrze b już nie

27 lip 14:51
Saizou : 1)
a=−8
b=22
2)
a=8
b=10
27 lip 14:56
rumpek: 
27 lip 14:57
rumpek: Wyznacz wszystkie wartości parametru m, dla których równanie 2x2 + (3 − 2m)x − m + 1 = 0 ma
dwa różne pierwiastki x1, x2 takie, że: |x1 − x2| = 3
27 lip 14:58
rumpek: Logarytmy już były

?
27 lip 15:00
Saizou : 
27 lip 15:04
rumpek: a szkoda

bo mam fajne dowody z tego działu

27 lip 15:05
Saizou : to najpierw wyznaczę sobie x
1−x
2
| | −b−√Δ | | −b+√Δ | | −b−√Δ+b−√Δ | | −2√Δ | | −√Δ | |
x1−x2= |
| − |
| == |
| = |
| = |
|
|
| | 2a | | 2a | | 2a | | 2a | | a | |
1
o
Δ>0
(3−2m)
2−4*2*(−m+1)>0
9−12m+4m
2+8m−8>0
4m
2−4m+1>0
(2m−1)
2>0
2
o
lx
1−x
2l=0
| −√(2m−1)2 | | −√(2m−1)2 | |
| =3 lub |
| =−3
|
| 2 | | 2 | |
l2m−1l=−6 l2m−1l=6
sprzeczność 2m−1=6 lub 2m−1=−6
27 lip 15:24
rumpek: ok, a postaraj się to |x
1 − x
2| = 3 rozpisać za pomocą Wzorów Viete'a

bo głównie o to tu
chodziło
27 lip 15:28
Saizou : √(x1−x2)2=3
(x1−x2)2=9
x22−2x1*x2+x22=9
(x1+x2)2−4x1*x2=9
27 lip 15:32
rumpek: ok

27 lip 15:33
rumpek: Wykaż, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
27 lip 15:40
Saizou :
na razie mam rysunek

27 lip 15:52
Eta:
Witam
Saizou 
Na początek
łatwe 
1/ wykaż, że liczba 5
12−1 jest podzielna prze
21
2/ Wykaż,że liczba
√6−2√5 −
√5 jest całkowita
27 lip 15:54
Saizou : Witaj Eto na razie walczę z dowodem
27 lip 15:55
Eta:
| | 1 | |
3/ Wiedząc,że liczba "a" jest rozwiązaniem równania x+ |
| =5 , dla x≠0 |
| | x | |
| | 1 | |
Podaj wartość wyrażenia : a3+ |
| bez wyznaczania liczby "a" |
| | a3 | |
27 lip 15:57
Eta:
Ok

mnie się nie śpieszy

27 lip 15:58
rumpek: chyba za łatwe

27 lip 16:01
Saizou :
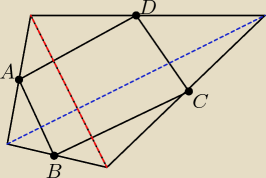
to za pomocą Talesa można udowodnić, że lABl i lDCl i czerwona przekątna są równoległe oraz, że
lADl i lBCl i niebieska przekątna są równoległe, zatem z definicji równoległoboku, że jest to
figura która ma 2 pary boków równoległych można to udowodnić
27 lip 16:03
rumpek: to nie dowód

27 lip 16:05
rumpek: + czworokąty dzielą się na: ...
27 lip 16:05
Saizou : trapezy, trapezoidy i równoległoboki
27 lip 16:08
rumpek: wypukłe i ...

27 lip 16:09
Mila: Saizou, jeśli chcesz dostać pełną pulę punktów za to zadanie, to rozpisz.
1) założenie
2) teza
3) dowód, dokładnie z jakich własności korzystasz, jakie własności równoległoboku chcesz
wykazać.( korzystasz z twierdzenia odwrotnego do...)
27 lip 16:09
Saizou : wypukłe
27 lip 16:10
Saizou : i wklęsłe
27 lip 16:11
rumpek: 
pamiętaj o tym i o tym co dostałeś w poście od Mili

że korzystasz z twierdzenia
odwrotnego do Talesa

a nie tw. Talesa samego

27 lip 16:14
pigor: ... a mnie "męczyło" to zadanie :
Udowodnij że n5 − n jest podzielne przez 5,
no bo co zrobić jakbym nie wpadł na to, że
n2+1=n2−4+5=... i dalej wiadomo, otóż tak:
prosto dochodzę do
n5−n= n(n−1)(n+1)(n
2+1) , no a jasne jest, że liczba n za cyfrę
jedności może mieć cyfrę ze zbioru {0,1,2,3,4,5,6,7,8,9} , przy tym
jeśli kończy się jedną z cyfr
0,1,4,5,6,9 , to wtedy 5 dzieli jedną z trzech liczb
iloczynu n(n−1)n+1), czyli 5|n albo 5|(n−1) albo 5|(n+1) (kończy się zerem albo 5),
natomiast
jeśli n za cyfrę jedności ma jedną z cyfr
2,3,7,8 , to n
2 kończy się cyfrą 4 albo 9, a
wtedy 5|(n
2+1) , a to wyczerpuje wszystkie możliwości c.n.w. . ...

27 lip 16:15
rumpek: pigor odnośnie tego n
5 − n to ja jednak zastosowałbym małe twierdzenie Fermata

migiem
się robi

27 lip 16:20
rumpek: lub alternatywny sposób:
n
5 − n = n(n
4 − 1) = n(n
2 − 1)(n
2 + 1) = n(n − 1)(n + 1)(n
2 + 1) = n(n − 1)(n + 1)(n
2 − 4
+ 5) =
= 5n(n − 1)(n + 1) + n(n − 1)(n + 1)(n
2 − 4) = 5n(n − 1)(n + 1) + n(n − 1)(n − 2)(n + 1)(n +
2)
czyli pierwszy element [5n(n − 1)(n + 1)] dzieli się przez 5 wiadomo

oraz drugi element
[n(n − 1)(n − 2)(n + 1)(n + 2)] to jest 5 kolejnych liczb

więc jedna dzieli się przez 5
27 lip 16:22
Eta:

27 lip 16:23
Krzychu: A może być taka odpowiedź: liczba n5−n jest podzielna przez 5 i wynika to z małego twierdzenia
Fermata.
27 lip 16:23
rumpek: teoretycznie
Krzychu może być, jednak ja przeprowadziłbym dowód

zależy od klucza
27 lip 16:24
Eta:
Ja bym tak napisała

bo nie każą podać dowodu tw, Fermata

27 lip 16:25
Krzychu: rumpek, a mógłbyś przedstawić tutaj dowód?
27 lip 16:30
27 lip 16:32
Eta:


27 lip 16:36
Krzychu: ten indukcyjny?
Ma ktoś może pdf/strona z nauką od podstaw modulo?
27 lip 16:37
Saizou : oświećcie mnie z tym dowodem

27 lip 16:44
rumpek: no Mila podała ci wskazówki, ja też napisałem że aby dostać pełną liczbę punktów nie wolno ci
uogólnić

27 lip 16:49
Mila: Saizou, o który dowód chodzi. Załóż nowy wątek, tak będzie lepiej.
Zadanie geometryczne.(dobry rysunek z 16:03)
Dobrze byłoby, zapamietać.
1) Odcinek łączący środki dwóch boków trójkąta jest jest równoległy do trzeciego boku i
równy jego połowie.
(To wynika z twierdzenia odwrotnego do tw. Talesa)
2) Masz wiedzieć: Co to jest równoległobok i jakie ma własności?
Co wystarczy wykazać, aby czworokąt był równoległobokiem?
27 lip 17:01
Krzychu: Mila: a dowód MTF to ten przeprowadzony indukcyjnie w tym załączonym poście?
27 lip 17:16
rumpek: Krzychu tak ten post
Basi przedostatni post

27 lip 17:18
krzys: 4 1/2 + ( 3 x 2 3/4) =?
28 lip 17:38
Kacper:
biorę

21 sty 08:33






 11! = 11*10*9*8*7*6*5*4*3*2 = 28*34*52*71*111
a więc dzielnik liczby 11! musi być postaci: 2a3b5c7d11e
gdzie:
a= 0,1,2,3,4,5,6,7,8
b= 0,1,2,3,4
c= 0,1,2
d= 0,1
e= 0,1
ile różnych takich zestawów możesz zrobić
11! = 11*10*9*8*7*6*5*4*3*2 = 28*34*52*71*111
a więc dzielnik liczby 11! musi być postaci: 2a3b5c7d11e
gdzie:
a= 0,1,2,3,4,5,6,7,8
b= 0,1,2,3,4
c= 0,1,2
d= 0,1
e= 0,1
ile różnych takich zestawów możesz zrobić  Tyle że wtedy liczb dzielników będzie o wiele wiele wiele mniejsza niż sugerowana przez Etę.
Tyle że wtedy liczb dzielników będzie o wiele wiele wiele mniejsza niż sugerowana przez Etę.







 Myślałam, że jesteś przyszłorocznym maturzystą z rozszerzeniem
Myślałam, że jesteś przyszłorocznym maturzystą z rozszerzeniem 
 gdzie z taką niewiedzą
gdzie z taką niewiedzą
 teraz zauważyłam,że napisałeś 1 LO rozszerzony
teraz zauważyłam,że napisałeś 1 LO rozszerzony 


 a teraz wezmę się za 10
a teraz wezmę się za 10
 Zad.8 x=2 i y=7 v x=7 i y=2 v x=3 i y=4 v x=4 i y=3
Zad.8 x=2 i y=7 v x=7 i y=2 v x=3 i y=4 v x=4 i y=3
 ( nie przeczytałam ... pomyślałam o naturalnych
( nie przeczytałam ... pomyślałam o naturalnych 
 W = −3
Wx = 1 − 2k
Wy = k − 2
W = −3
Wx = 1 − 2k
Wy = k − 2

 Zad :
W kąt o mierze 60o wpisano koło, a następnie dopisano jeszcze cztery koła tak, że każde
następne jest styczne zewnętrznie do poprzedniego i do ramion kąta.
a)uzasadnij, że długości promieni tych kół tworzą ciąg geometryczny.
b)oblicz, ile razy suma pól wszystkich pięciu kół jest większa od pola najmniejszego koła.
Zad :
W kąt o mierze 60o wpisano koło, a następnie dopisano jeszcze cztery koła tak, że każde
następne jest styczne zewnętrznie do poprzedniego i do ramion kąta.
a)uzasadnij, że długości promieni tych kół tworzą ciąg geometryczny.
b)oblicz, ile razy suma pól wszystkich pięciu kół jest większa od pola najmniejszego koła.















 W tym zadaniu są same podstawy ciągów.
W tym zadaniu są same podstawy ciągów.
 y≥lxl−2 i lyl≤1
y≤1 i y≥−1 i teraz narysuję sobie funkcje y=−1 i y=1 oraz funkcję y=lxl i przesunę ją o 2
jednostki w dół, zatem y∊<−1:1> ,a x∊<−3:−1>∪<1:3>
y≥lxl−2 i lyl≤1
y≤1 i y≥−1 i teraz narysuję sobie funkcje y=−1 i y=1 oraz funkcję y=lxl i przesunę ją o 2
jednostki w dół, zatem y∊<−1:1> ,a x∊<−3:−1>∪<1:3>
 nie do końca dobrze to jest
proste i wykres w porządku
teraz
−1 ≤ y ≤ 1
to pas między prostymi (razem z nimi)
a
y ≥ |x|−2
to to czerwony wykres plus to co powyżej niego
fioletowe to część wspólna czyli rozwiązanie układu
nie do końca dobrze to jest
proste i wykres w porządku
teraz
−1 ≤ y ≤ 1
to pas między prostymi (razem z nimi)
a
y ≥ |x|−2
to to czerwony wykres plus to co powyżej niego
fioletowe to część wspólna czyli rozwiązanie układu

 czyli rysuję prostą y=2 oraz funkcje y=x−2 i y=x+2 czyli rozwiązanie to obszar zielony z
różowymi liniami, ale bez pomarańczowej
czyli rysuję prostą y=2 oraz funkcje y=x−2 i y=x+2 czyli rozwiązanie to obszar zielony z
różowymi liniami, ale bez pomarańczowej

 zaraz policzymy spokojnie
zaraz policzymy spokojnie
 Która z liczb jest większa: 2791 czy 5339
Która z liczb jest większa: 2791 czy 5339







 a teraz wszystkim życzę miłej nocy
a teraz wszystkim życzę miłej nocy



 za poświęcony czas
za poświęcony czas


 i za to
i za to 

 swoją drogą zaimek nikt się nie odmienia
swoją drogą zaimek nikt się nie odmienia
 Według mnie są najłatwiejszym materiałem przerabianym w II klasie liceum
Według mnie są najłatwiejszym materiałem przerabianym w II klasie liceum 




 Jak widać zadanko nie było takie trudne
Jak widać zadanko nie było takie trudne 

 to co może jeszcze jedno zadanie
to co może jeszcze jedno zadanie np. na dowód
np. na dowód


 tworzę nową matematykę
tworzę nową matematykę 

 Takie proste zadanko z matury.
Takie proste zadanko z matury.
 pierwiastki
pierwiastki 


 ?
?

 bo mam fajne dowody z tego działu
bo mam fajne dowody z tego działu 
 bo głównie o to tu
chodziło
bo głównie o to tu
chodziło

 na razie mam rysunek
na razie mam rysunek 
 Na początek łatwe
Na początek łatwe  1/ wykaż, że liczba 512−1 jest podzielna prze 21
2/ Wykaż,że liczba √6−2√5 − √5 jest całkowita
1/ wykaż, że liczba 512−1 jest podzielna prze 21
2/ Wykaż,że liczba √6−2√5 − √5 jest całkowita
 mnie się nie śpieszy
mnie się nie śpieszy 

 to za pomocą Talesa można udowodnić, że lABl i lDCl i czerwona przekątna są równoległe oraz, że
lADl i lBCl i niebieska przekątna są równoległe, zatem z definicji równoległoboku, że jest to
figura która ma 2 pary boków równoległych można to udowodnić
to za pomocą Talesa można udowodnić, że lABl i lDCl i czerwona przekątna są równoległe oraz, że
lADl i lBCl i niebieska przekątna są równoległe, zatem z definicji równoległoboku, że jest to
figura która ma 2 pary boków równoległych można to udowodnić


 pamiętaj o tym i o tym co dostałeś w poście od Mili
pamiętaj o tym i o tym co dostałeś w poście od Mili  że korzystasz z twierdzenia
odwrotnego do Talesa
że korzystasz z twierdzenia
odwrotnego do Talesa  a nie tw. Talesa samego
a nie tw. Talesa samego 

 migiem
się robi
migiem
się robi 
 oraz drugi element
[n(n − 1)(n − 2)(n + 1)(n + 2)] to jest 5 kolejnych liczb
oraz drugi element
[n(n − 1)(n − 2)(n + 1)(n + 2)] to jest 5 kolejnych liczb  więc jedna dzieli się przez 5
więc jedna dzieli się przez 5

 zależy od klucza
zależy od klucza
 bo nie każą podać dowodu tw, Fermata
bo nie każą podać dowodu tw, Fermata





