Bryła obrotowa z przekątnej sześciokąta. BigMax: Zadanie jest zbyt hardcorowe jak dla mnie. Mój mózg nie potrafi tak w 3d operować: Oblicz pole powierzchni bryły obrotowej otrzymanej przez obrót sześciokąta foremnego o boku a wokół prostej zawierającej dłuższą przekątna sześciokąta. Z góry dziękuje za pomoc

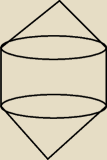
pazio: rysunek wyszedł trochę krzywo, ale ogólny zamysł chyba zawarł

	a√3
promień walca/stożków: r ⋀ r =
	2

powierchnia boczna walca: P_w

	a√3
Pw = 2π*		*a = a*π*√3
	2

powierchnie boczne stożków: P_s P_s = 2*π*r*l gdzie l=a

	a√3
Ps = 2π*		*a = a*π*√3
	2

P_w + P_s = 2*a*π*√3

pazio: nie a tylko a² przepraszam za błąd

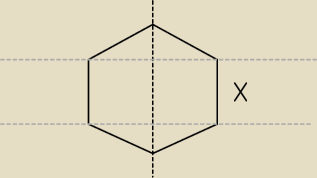
Jacek Karaśkiewicz: Długość boku − x. Czarna linia przerywana to oś obrotu, linie szare − pomocnicze. Otrzymana bryła obrotowa będzie "złożeniem" dwóch stożków i walca (szare linie wyznaczają płaszczyznę "złożenia" tych brył. Z obliczeniem pola powierzchni stożków i walca nie będziesz miał problemu. Pole powierzchni szukanej bryły jest sumą tamtych pól (pamiętaj tylko, że musisz policzyć pola powierzchni bocznych stożków i walca).

Jacek Karaśkiewicz: Spóźniłem się. Niezły rysunek, pazio

Bogdan:

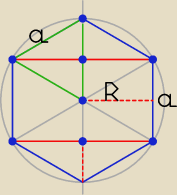
	1
Bryła składa się z walca o promieniu podstawy R =		a√3 (to jest wysokość
	2

trójkąta równobocznego o boku a) i wysokości a oraz z dwóch stożków o promieniach

	1
podstawy R i wysokości równej		a. Tworzące stożków mają długość a.
	2

Bogdan: Ja też się spóźniłem

pazio: dziekuje, jacku staralam sie jak moglam za to rysunek bogdana wymiata

lola95: W rozwiązaniu "pazio" powinno być chyba w wyniku końcowym P_w + 2 * P_s = 3*a²*π*√3 Przecież są dwa stożki.

lola95: Cofam honor Wszystko jest dobrze. Przepraszam za zamieszanie.