Pomoc z parametrem nameless: Rozwiąż równanie w parametrem m i przeprowadź dyskusję liczby jego rozwiązań: |x+5|+|x−3|=m Przyrównywałem m do zera, np że jeśli m<0 to równanie jest sprzeczne itd, jednak w odpowiedzi jak sprawdzałem przyrównują do liczby 8 np że jeśli m>8 to nieskończenie wiele rozwiązań, że jeśli m=8 to........ , m<8 to....... Chciałem, byscie mi pomogli zrozumieć w czym rzecz, chce zrozumieć ten sposób− mam jeszcze inne takie przykłady, które potem sam postaram się zrobić

Saizou : to najlepiej narysować funkcję f(x)=lx+5l+lx−3l następnie odczytać z wykresu dla jakiego parametru m funkcja ma 0 rozwiązań, 2 rozwiązania, nieskończenie wiele

Artur_z_miasta_Neptuna: kiedy |x+5| = 0 gdy x=−5 ... gdy x=−5 to |x−3| = |−5−3|=8 kiedy |x−3| = 0 gdy x=3 ... gdy x=3 tp |x+5| = |3+5| = 8 wniosek z tego jest następujący −−− minimalna wartość sumy = 8 wartość tej sumy =8 dla x∊<−5;3> ... czyli dla m=8 jest NIESKOŃCZENIE WIELE ROZWIĄZAŃ dla m<8 jest brak rozwiązań dla m>8 będą dwa rozwiązania (co wynika z wartości bezwzględnej)

nameless: Twój sposób Artur najbardziej mi odpowiada, dzięki wielkie

Artur_z_miasta_Neptuna: moje 'rozwiązanie' jest godne rozpatrzenia wtedy i tylko wtedy, gdy kojarzysz jak wygląda wykres funkcji f(x) = |x−coś| + |x−inne coś| ściągawka: http://www.wolframalpha.com/input/?i=plot%5B%7Cx%2B5%7C%3B%7Cx-3%7C%3B%7Cx%2B5%7C%2B%7Cx-3%7C%5D

Mila: |x+5|+|x−3|=m Metoda graficzna. f(x) =|x+5|+|x−3| y=m ( prosta pozioma) |x+5|=x+5 dla x≥−5 |x+5|=−x−5 dla x<−5 |x−3|=x−3 dla x≥3 |x−3|=−x+3 dla x<3 ustalam wzór f(x) w przedziałach (−∞,−5),<−5,3),<3,∞) 1) f(x)=−x−5−x+3=−2x−2 dla x z przedziału (−∞,−5) 2) f(x)=x+5−x+3=8 dla x z przedzialu <−5,3) 3) f(x)=x+5+x−3=2x+2 dla x z przedziału <3,∞) Narysu wykres tej funkcji. Czy potrafisz odczytać liczbę rozwiązań równania; |x+5|+|x−3|=m ?

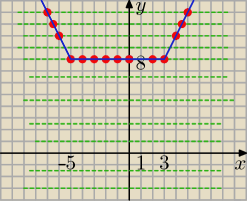
Eta: Wykres funkcji f(x) (wyznaczonej przez Milę { −2x−2 dla x€ ( −∞, −5) [N [f(x)]] = { 8 dla x€ <−3,3) { 2x+2 dla x€ <−3,∞) prosta y=m ma z wykresem f(x) (czerwone punkty wspólne odp: 0 rozwiązań dla m€ ( −∞, 8) 2 rozwiązania dla m€ ( 8,∞) nieskończenie wiele rozwiązań dla m=8

Mila: Eto, wiedziałam, że narysujesz.