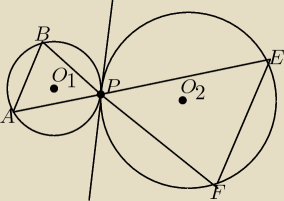 Proszę bardzo o pomoc w takim zadaniu:
Okrąg o środku O1 jest styczny do okręgu o środku O2 w punkcie P. Punkty A i B leżą na okręgu o
środku O1, a punkty E i F − na okręgu o środku O2 w taki sposób, że odcinki AE i BF przecinają
się w punkcie P (jak na rys.) Uzasadnij, ze trójkąty ABP i EFP są podobne.
Mam pytanie, czy cięciwy AB i EF są tu równoległe? Jeśli tak , to skąd to wynika?
Bo gdyby były równoległe , to dowód byłby prosty − na podstawie cechy kkk.
Proszę bardzo o pomoc w takim zadaniu:
Okrąg o środku O1 jest styczny do okręgu o środku O2 w punkcie P. Punkty A i B leżą na okręgu o
środku O1, a punkty E i F − na okręgu o środku O2 w taki sposób, że odcinki AE i BF przecinają
się w punkcie P (jak na rys.) Uzasadnij, ze trójkąty ABP i EFP są podobne.
Mam pytanie, czy cięciwy AB i EF są tu równoległe? Jeśli tak , to skąd to wynika?
Bo gdyby były równoległe , to dowód byłby prosty − na podstawie cechy kkk.
 zacznij od tego, że kąty trójkątów przy P są takie same
zacznij od tego, że kąty trójkątów przy P są takie same  ogólnie masz wykazać, że:
ogólnie masz wykazać, że:
| AP | BP | AB | |||
= | = | ||||
| EP | FP | EF |
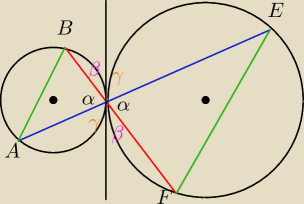 Równość kątów łatwo wykazać (tw. o przecięciu dwóch prostych)
Stąd wykazujesz, że BP ∼ FP oraz AP ∼ EP
natomiast podobieństwo AB ∼ EF można np, z tw. cosinusów (tutaj zgaduję)
Równość kątów łatwo wykazać (tw. o przecięciu dwóch prostych)
Stąd wykazujesz, że BP ∼ FP oraz AP ∼ EP
natomiast podobieństwo AB ∼ EF można np, z tw. cosinusów (tutaj zgaduję)
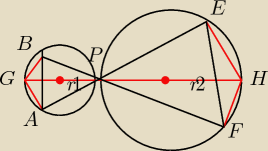 Kąty BPA= FPE. Kąty GPB=GAP=PEH=PFH=90 jako oparte na srednicy, kąty BPG=FPH i GPA=EPH czyli
trójkąty GBP i FPH są podobne oraz AGP i PEH też podobne /mają trzy jednakowe kąty/, a więc
BP/2*r1=PF/2*r2 czyli BP/PF=2*r1/2*r2, analogicznie AP/PE=r1/r2, z tego wynika
BP/PF=AP/PE=r1/r2. Więc trójkąty APB i EFP posiadają równy kąt i proporcjonalne dwa boki cnd.
Kąty BPA= FPE. Kąty GPB=GAP=PEH=PFH=90 jako oparte na srednicy, kąty BPG=FPH i GPA=EPH czyli
trójkąty GBP i FPH są podobne oraz AGP i PEH też podobne /mają trzy jednakowe kąty/, a więc
BP/2*r1=PF/2*r2 czyli BP/PF=2*r1/2*r2, analogicznie AP/PE=r1/r2, z tego wynika
BP/PF=AP/PE=r1/r2. Więc trójkąty APB i EFP posiadają równy kąt i proporcjonalne dwa boki cnd.