witam , potrzebuje pomocy czarodziej: Wyznacz te wartości parametru m (m∊R) dla których:

	3
zbiór rozwiązań nierówności		≥ 1 zawiera się w zbiorze rozwiązań nierówności
	x+1

(m+1)x² − (3m+4)x + 3 ≥ 0

Basia: rozwiąż najpierw nierówność

3
	≥ 1
x+1

potrafisz ? jeżeli tak podaj wynik

czarodziej: wyszło mi że x∊(−1;2) tylko przedział zamknięty tylko niewiem jak go napisać, tyle jeszcze umiem ale teraz wogóle niewiem od czego zacząć , niewiem jak patrzeć na te przypadki

Artur z miasta Neptuna: no to teraz: dla jakiego parametru 'm' nierówność: (m+1)x²−(3m+4)x+3≥0 ⇔ a(x+1)(x−2)≥0 ... dla a<0 ... czyli a = (m+1) jak to obliczyć najlepiej WZORY VIETE'A

Jack: zastanawiam się, Artur, do czego zmierzasz i skąd wziąłeś równoważność...

Saizou : i jeszcze trzeba rozpatrzeć nierówność liniowej dla a=0, zatem m+1=0→m=−1 −(3*(−1)+4)x+3≥0 −(−3+4)x+3≥0 −(1)x≥−3 x≤3

Saizou : i funkcja kwadratowa 1^o a>0 m+1>0 m>−1 2^o Δ≥0 [−(3m+4)]²−4(m+1)*3≥0 9m²+24m+16−12m−12≥0 9m²−8m≥0

	8
m(9m−8)≥0→m∊(−∞:0>∪<		:+∞)
	9

Saizou : znalazłem błąd 9m²+24m+16−12m−12≥0 i już piszę poprawkę

Saizou : 9m²+12m+4≥0 (3m+2)²≥0→m∊R

czarodziej: kurcze bardzo dziękuje za odpowiedź ale moglibyście mi te warunki zapisać wszystko za jednym razem bo sie cały czas gubie i jeszcze wogóle nie rozumiem co zrobił Artur z miasta Neptuna , wogóle niewiem skąd to sie wzięło , proszę o wyjaśnienie

Artur z miasta Neptuna: Nie patrz na to co napisalem − bo to co napisalem odnosilo sie do zadania w ktorym oba rozwiazania mialyby byc identyczne − stad z rozwoazania pierwszej nierownosci bylo wywnioskowane rozwiazanie drugiej nierownosci

Basia: bałagan zrobił się tu straszny; zróbmy zatem porządek, ale to trochę potrwa na początek umówmy się, że: A = (−1;2> B = zbiór rozwiązań nierówności (m+1)x² − (3m+4)x + 3 ≥ 0 x₁ < x₂ (jeżeli mamy dwa różne pierwiastki, bo przecież zawsze można zamienić oznaczenia gdyby wyszło inaczej) reszta będzie za chwilę

Basia: 1. m+1 = 0 ⇔ m= −1 wtedy mamy: 0*x² − (−3+4)x + 3 ≥ 0 −x + 3 ≥ 0 −x ≥ −3 /*(−1) x ≤ 3 B = (−∞; 3> A⊂B czyli m = −1 spełnia warunki zadania 2. m+1 ≠ 0 ⇔ m≠ −1 wtedy Δ = [−(3m+4)]² − 4(m+1)*3 = 9m² + 24m + 16 − 12m − 12 = 9m² + 12m + 4 = (3m+2)² zatem Δ ≥ 0 dla każdego m∊R 2.1 Δ=0 Δ=0 ⇔ 3m+2=0 ⇔ m = −²₃ wtedy a=m+1 = ¹₃

	−b		3m+4		2
parabola ramionami do góry; x0 =		=		=		= 3
	2a		2(m+1)		23

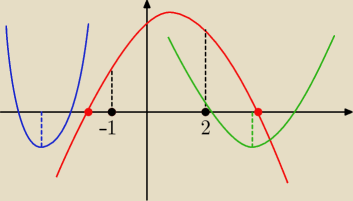
naszkicuj ją sobie B = R A⊂B czyli m = −²₃ spełnia warunki zadania 2.2 m < −1 wtedy Δ > 0 i mamy parabolę ramionami w dół (czerwona) B = <x₁; x₂> aby A ⊂ B musi być: x₁ ≤ −1 i x₂ ≥2 aby ten warunek był spełniony wystarczy aby f(−1)≥0 i f(2) ≥ 0 czyli (m+1)(−1)² − (3m+4)(−1)+ 3 ≥ 0 m+1+3m+4+3 ≥0 4m+8 ≥ 0 m ≥ −2 i (m+1)*2² − (3m+4)*2+ 3 ≥ 0 4m+4−6m−8+3 ≥0 −2m−1 ≥ 0 −2m ≥ 1 m ≤ −¹₂ czyli mamy trzy warunki: m < −1 m ≥ −2 m ≤ −¹₂ co daje nam m∊<−2; −1) 2.3 m > −1 i m≠ −²₃ wtedy Δ > 0 i mamy parabolę ramionami do góry (niebieska lub zielona) B = (−∞;x₁>∪<x₂;+∞) aby A ⊂ B musi być: x₁ ≤ −1 i x₂ ≤ −1 (niebieska) lub x₁≥2 i x₂≥2 (zielona) aby te warunki był spełnione wystarczy aby

	b
f(−1)≥ 0 i p = −		< −1
	2a

lub

	b
f(2)≥0 i p = −		> 2
	2a

czyli (m+1)(−1)² − (3m+4)(−1)+ 3 ≥ 0 m+1+3m+4+3 ≥0 4m+8 ≥ 0 m ≥ −2 i

	−(3m+4)
−		< −1
	2(m+1)

3m+4
	< −1 /*2(m+1)
2(m+1)

2(m+1) jest dodatnie bo rozważam przypadek m>−1 3m+4 < −2(m+1) 5m < −6 m < −⁶₅ sprzeczność lub (m+1)*2² − (3m+4)*2+ 3 ≥ 0 4m+4−6m−8+3 ≥0 −2m−1 ≥ 0 −2m ≥ 1 m ≤ −¹₂ i

	−(3m+4)
−		> 2
	2(m+1)

3m+4
	> 2 /*2(m+1)
2(m+1)

2(m+1) jest dodatnie bo rozważam przypadek m>−1 3m+4 > 4(m+1) −m > 0 m < 0 czyli mam trzy warunki m > −1 m≤ − ¹₂ m < 0 co daje mi m∊(−1; − ¹₂> pozbieraj to teraz razem i ładnie zapisz jakie m spełniają warunki zadania

Basia: P.S. i dokładnie posprawdzaj obliczenia, bo mogłam się gdzieś w prostych rachunkach pomylić

Jack: oszczędziłaś mi, Basiu, rozpisywania przypadków... Sam początek marnie szedł i liczyłem że ktoś pociągnie temat Wakacyjne lenistwo..

czarodziej:

	1
czyli m ∊ <−2;−		>
	2

wielkie dzięki za zapisanie tego wszystkiego razem