Ułamki z dwiema niewiadomymi
Grzesiek: Naszkicuj i zapisz rozwiązania równań z dwiema niewiadomymi*:
a) IxI / IyI = 0
b) IxI / IyI = 1
c) IxI / IyI = −1
d) IxI / IyI = IxI
e) IxI / IyI = IyI
* w zadaniach zastąpiłem kreskę ułamkową tym znakiem / bo nie umiem wstawić ułamka
21 lip 17:11
Basia: przeczytaj "instrukcję obsługi":
https://matematykaszkolna.pl/forum/przyklady9.html
ad.b,c,e
rozbijasz na przypadki:
1. x≥ 0 i y>0
2. x≥0 i y<0
3. x<0 i y>0
4. x<0 i y<0
(czyli na poszczególne ćwiartki bez osi OX bo y≠0)
i patrzysz co będzie
ad.a
| |x| | |
| = 0 ⇔ |x| = 0 ⇔ x=0 i y dowolne, ale ≠0 |
| |y| | |
to Ci daje oś OY bez punktu (0,0)
ad.d
| |x| | |
| = |x| ⇔ |x| = 0 lub |y|=1 |
| |y| | |
spróbuj dokończyć
21 lip 17:19
Grzesiek: ad a
dlaczego bez punktu (0,0) ?
ad d
Czy będzie dobrze
x = 0 lub y = 1 lub y = −1

?
tylko jak graficznie przedstawić rozwiązanie?
21 lip 17:27
Basia:
bo |y| jest w mianowniku, a mianownik musi być ≠ 0 czyli |y|≠0 czyli y≠0 czyli
odpadają wszystkie punkty (x;0)
a więc także (0,0)
ad.b
dobrze
graficznie to jest jak poprzednio oś OY bez (0,0)
plus prosta y=1 plus prosta y=−1
czyli proste równoległe do OX przechodzące odpowiednio przez (0,1) i (0,−1)
21 lip 17:32
Grzesiek: Czyli idąc dalej
przykład b
| IxI | |
| = 1 ⇔ |x| = 0 ⇔ x=0 i y=x, ale ≠0 |
| IyI | |
a graficznie to już nie wiem
przykład e
| IxI | |
| = IyI ⇔ |x| = 1 ⇔ x = 1 lub x = −1 |
| IyI | |
ale co z y
21 lip 17:53
Basia:
nie; co innego =0; co innego = 1
zero jest specyficzne, dla 1 już to tak nie działa
rozbijasz na przypadki:
1.
x≥0 i y>0 (I ćwiartka bez OX)
wtedy |x| = x i |y| = y
i masz
y = x
rysujesz kawałek tej prostej w I ćwiartce znowu bez (0,0)
2.
x≥0 i y<0 (IV≥ ćwiartka bez OX)
wtedy |x| = x i |y| = −y
i masz
y = −x
rysujesz kawałek tej prostej w IV ćwiartce znowu bez (0,0)
3.
x<0 i y>0 (czyli II ćwiartka)
|x| = −x |y| = y
y = −x
rysujesz kawałek tej prostej w II ćwiartce znowu bez (0,0)
4.
x<0 i y<0 czyli III ćwiartka
|x| = −x i |y| = −y
y = x
rysujesz kawałek tej prostej w III ćwiartce znowu bez (0,0)
ostatecznie masz sumę prostych y=x i y= −x bez punktu (0,0)
pozostałe przykłady identycznie
21 lip 18:05
Mila:
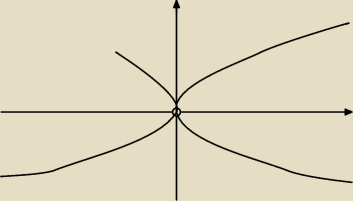
e) Suma parabol bez (0,0)
x=y
2 lub x=−y
2
21 lip 18:06
sikora: I skąd ten wniosek w przykładzie e tak w ogóle?
A w d że |x|=0 ?
21 lip 18:09
Basia:
w przykładzie
nie było potrzeby takiego rozbijania, bo wiadomo, że
ułamek = 0 ⇔ licznik =0
dla
już żadnej takiej zależności nie ma
analogicznie w przykładzie
nie ma potrzeby rozbijania
bo ta równość może zachodzić ⇔
1. |x| = 0 (wtedy obie strony = 0)
lub
2. |x| ≠ 0
dzielimy przez |x|
i mamy
|y| = 1
ale w przykładzie (e) to już tak nie działa
21 lip 18:11
Maslanek: Nie trzeba rozpatrywać czterech przypadków.
|x|=|y| ⇔ x=y lub x=−y.
Czyż nie?
21 lip 18:17
pigor: tak , masz rację ...

nie trzeba rozpatrywać 4−ech przypadków

21 lip 18:23
Mila: c.d.( e)
| | IxI | |
e) |
| = IyI /*|y|, y≠0 |
| | IyI | |
y
2=|x|
x=y
2 lub x=−y
2 parabole, osią symetrii jest oś OX.
21 lip 22:15
Grzesiek: Dziękuję wszystkim za pomoc, niestety tak jak myślałem baba się na mnie uwzięła − nie
zaliczyłem



Zadania, które już wysyłam po raz n−ty (początkowo sam próbowałem rozwiązywać)
wróciły bo "nie ma w ogole algebraicznego zapisu rozwiązania" + inne komentarze:
Ad. a) b) d)
Komentarz "Brak zapisu rozwiązania

! Podobnie w pozostałych przypadkach. Czyli znowu to samo,
co było w poprzedniej wersji

! "
Ad. c)
|y|= −|x|
dla: x>=0 i y>=0 y= −x
dla: x<0 i y<0 y= −x
dla: x>=0 i y<0 y= x
dla: x<0 i y>=0 y=x
Funkcja nie ma rozwiązań w zbiorze liczb rzeczywistych, nie ma wykresu
Komentarz: "Funkcja nigdy nie ma rozwiązań. Równanie ma zawsze rozwiązanie."
Drugie zadanie też wróciło nie zaliczone:
.Rozwiąż równanie |5+xy|=5+xy, traktując je jako:
a) równanie z dwiema niewiadomymi,
b) równanie z niewiadomą x i parametrem y
Ad. a)
|5+xy| = 5+xy ⇔ 5+xy≥0 ⇔ xy ≥ −5
Komentarz: "Do tego miejsca przejścia były równoważne. A co się dzieje tutaj

?"
x=0 ⇒ 0*y = 0 ≥ −5
czyli mamy całą oś 0Y
x>0 ⇒ y≥ −
czyli mamy całą I ćwiartkę + to co leży w IV ćwiartce powyżej ramienia hiperboli + ramię
hiperboli
x<0 ⇒ y≤ −
czyli mamy całą III ćwiartkę i to co w II leży poniżej ramienia hiperboli + ramię hiperboli
Komentarz" Brak zapisu rozwiązania

!
Elementarne błędy językowe!"
Ad. b)
|5+xy| = 5+xy ⇔ 5+xy≥0 ⇔ xy ≥ −5
i teraz rozważamy przez przypadki w zależności od wartości parametru y:
1. y=0
Komentarz "A jaki tu jest znak logiczny w stosunku do ostatniej nierówności

?"
0≥ −5
czyli dla y=0 zbiorem rozwiązań jest R
Komentarz "Nie „zbiorem rozwiązań” tylko „rozwiązaniem” lub „zbiorem pierwiastków”.
2. y>0
x≥ czyli xЄ <− ; +
∞)
3. y<0
x≤ czyli xЄ (−
∞; − )
Komentarz "Brak zapisu rozwiązania. W tym zadaniu różnica w zapisie rozwiązania w obu
przypadkach jest kluczowa. Bo metoda rozwiązania się nie zmienia. Proszę porządnie uzupełnić
ten zapis, tak, żeby pokazywał na czym polega istota różnicy między przypadkami a) i b). "
I jak tu lubić matematykę

?
6 wrz 10:55
Mila: Do (e) jaki był komentarz?
Spróbuję Ci pomóc, ale nie wiem , jakie rozwiązania wysłałeś.
Może dołącz skan.
6 wrz 15:19
Grzesiek: Mila wstawiam linki do skanów, od pół roku próbuję zaliczyć te ćwiczenia, z 6 zadań zostały mi
dwa których nie mogę zaliczyć, dlatego zdecydowałem się poprosić o pomoc na forum ponieważ
moje rozwiązania są stale odrzucane. Najgorsze jest to, że nie wiem co robię źle.
Ostatnia wersja − którą wysłałem jest z tego forum i też odrzucono − bo "nie ma w ogole
algebraicznego zapisu rozwiązania" − to cytat z maila, reszta komentarzy jest na żółto w
skanach.
Wydawało mi się, że dojście do x i y to jest algebraiczne rozwiązanie, teraz już nic nie wiem.
http://wstaw.org/m/2012/09/06/skan_1.jpg
http://wstaw.org/m/2012/09/06/skan_2.jpg
http://wstaw.org/m/2012/09/06/skan_3.jpg
6 wrz 22:01
 ?
tylko jak graficznie przedstawić rozwiązanie?
?
tylko jak graficznie przedstawić rozwiązanie?
 e) Suma parabol bez (0,0)
x=y2 lub x=−y2
e) Suma parabol bez (0,0)
x=y2 lub x=−y2
 nie trzeba rozpatrywać 4−ech przypadków
nie trzeba rozpatrywać 4−ech przypadków 


 Zadania, które już wysyłam po raz n−ty (początkowo sam próbowałem rozwiązywać)
wróciły bo "nie ma w ogole algebraicznego zapisu rozwiązania" + inne komentarze:
Ad. a) b) d)
Komentarz "Brak zapisu rozwiązania
Zadania, które już wysyłam po raz n−ty (początkowo sam próbowałem rozwiązywać)
wróciły bo "nie ma w ogole algebraicznego zapisu rozwiązania" + inne komentarze:
Ad. a) b) d)
Komentarz "Brak zapisu rozwiązania ! Podobnie w pozostałych przypadkach. Czyli znowu to samo,
co było w poprzedniej wersji
! Podobnie w pozostałych przypadkach. Czyli znowu to samo,
co było w poprzedniej wersji ! "
Ad. c)
|y|= −|x|
dla: x>=0 i y>=0 y= −x
dla: x<0 i y<0 y= −x
dla: x>=0 i y<0 y= x
dla: x<0 i y>=0 y=x
Funkcja nie ma rozwiązań w zbiorze liczb rzeczywistych, nie ma wykresu
Komentarz: "Funkcja nigdy nie ma rozwiązań. Równanie ma zawsze rozwiązanie."
Drugie zadanie też wróciło nie zaliczone:
.Rozwiąż równanie |5+xy|=5+xy, traktując je jako:
a) równanie z dwiema niewiadomymi,
b) równanie z niewiadomą x i parametrem y
Ad. a)
|5+xy| = 5+xy ⇔ 5+xy≥0 ⇔ xy ≥ −5
Komentarz: "Do tego miejsca przejścia były równoważne. A co się dzieje tutaj
! "
Ad. c)
|y|= −|x|
dla: x>=0 i y>=0 y= −x
dla: x<0 i y<0 y= −x
dla: x>=0 i y<0 y= x
dla: x<0 i y>=0 y=x
Funkcja nie ma rozwiązań w zbiorze liczb rzeczywistych, nie ma wykresu
Komentarz: "Funkcja nigdy nie ma rozwiązań. Równanie ma zawsze rozwiązanie."
Drugie zadanie też wróciło nie zaliczone:
.Rozwiąż równanie |5+xy|=5+xy, traktując je jako:
a) równanie z dwiema niewiadomymi,
b) równanie z niewiadomą x i parametrem y
Ad. a)
|5+xy| = 5+xy ⇔ 5+xy≥0 ⇔ xy ≥ −5
Komentarz: "Do tego miejsca przejścia były równoważne. A co się dzieje tutaj ?"
x=0 ⇒ 0*y = 0 ≥ −5
czyli mamy całą oś 0Y
x>0 ⇒ y≥ −
czyli mamy całą I ćwiartkę + to co leży w IV ćwiartce powyżej ramienia hiperboli + ramię
hiperboli
x<0 ⇒ y≤ −
czyli mamy całą III ćwiartkę i to co w II leży poniżej ramienia hiperboli + ramię hiperboli
Komentarz" Brak zapisu rozwiązania
?"
x=0 ⇒ 0*y = 0 ≥ −5
czyli mamy całą oś 0Y
x>0 ⇒ y≥ −
czyli mamy całą I ćwiartkę + to co leży w IV ćwiartce powyżej ramienia hiperboli + ramię
hiperboli
x<0 ⇒ y≤ −
czyli mamy całą III ćwiartkę i to co w II leży poniżej ramienia hiperboli + ramię hiperboli
Komentarz" Brak zapisu rozwiązania !
Elementarne błędy językowe!"
Ad. b)
|5+xy| = 5+xy ⇔ 5+xy≥0 ⇔ xy ≥ −5
i teraz rozważamy przez przypadki w zależności od wartości parametru y:
1. y=0
Komentarz "A jaki tu jest znak logiczny w stosunku do ostatniej nierówności
!
Elementarne błędy językowe!"
Ad. b)
|5+xy| = 5+xy ⇔ 5+xy≥0 ⇔ xy ≥ −5
i teraz rozważamy przez przypadki w zależności od wartości parametru y:
1. y=0
Komentarz "A jaki tu jest znak logiczny w stosunku do ostatniej nierówności ?"
0≥ −5
czyli dla y=0 zbiorem rozwiązań jest R
Komentarz "Nie „zbiorem rozwiązań” tylko „rozwiązaniem” lub „zbiorem pierwiastków”.
2. y>0
x≥ czyli xЄ <− ; +∞)
3. y<0
x≤ czyli xЄ (−∞; − )
Komentarz "Brak zapisu rozwiązania. W tym zadaniu różnica w zapisie rozwiązania w obu
przypadkach jest kluczowa. Bo metoda rozwiązania się nie zmienia. Proszę porządnie uzupełnić
ten zapis, tak, żeby pokazywał na czym polega istota różnicy między przypadkami a) i b). "
I jak tu lubić matematykę
?"
0≥ −5
czyli dla y=0 zbiorem rozwiązań jest R
Komentarz "Nie „zbiorem rozwiązań” tylko „rozwiązaniem” lub „zbiorem pierwiastków”.
2. y>0
x≥ czyli xЄ <− ; +∞)
3. y<0
x≤ czyli xЄ (−∞; − )
Komentarz "Brak zapisu rozwiązania. W tym zadaniu różnica w zapisie rozwiązania w obu
przypadkach jest kluczowa. Bo metoda rozwiązania się nie zmienia. Proszę porządnie uzupełnić
ten zapis, tak, żeby pokazywał na czym polega istota różnicy między przypadkami a) i b). "
I jak tu lubić matematykę ?
?