 Nie rozumiem, w jakich sytuacjach, przy rozwiązywaniu trójkątów korzystając z twierdzenia
sinusów, rozpatrujemy dwa przypadki. Podam to na przykładzie zadania:
Rozwiąż trójkąt ABC, jeśli:
a=12
b=16
α=30*
Odp:c=22,8, β=42, γ=108 >LUB< c=5, β=138, γ=12
To chyba ma związek z tym, że sinus jest dodatni w przedziale (0*;180*), ale to wszystko co
wiem.
Nie rozumiem, w jakich sytuacjach, przy rozwiązywaniu trójkątów korzystając z twierdzenia
sinusów, rozpatrujemy dwa przypadki. Podam to na przykładzie zadania:
Rozwiąż trójkąt ABC, jeśli:
a=12
b=16
α=30*
Odp:c=22,8, β=42, γ=108 >LUB< c=5, β=138, γ=12
To chyba ma związek z tym, że sinus jest dodatni w przedziale (0*;180*), ale to wszystko co
wiem.
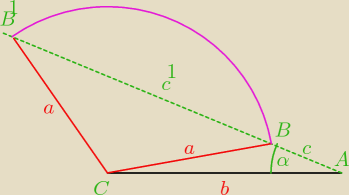 ... to poprostu wynika z faktu że można skonstruować "na tych danych" dwa różne trójkąty.
(odkładasz bok b ... z jednego końca kreślisz kąt α=30o ... z drugiego końca promieniem
równym a szukasz wierzchołków B i Bi)
... to poprostu wynika z faktu że można skonstruować "na tych danych" dwa różne trójkąty.
(odkładasz bok b ... z jednego końca kreślisz kąt α=30o ... z drugiego końca promieniem
równym a szukasz wierzchołków B i Bi)
| 2 | ||
Jak wyszła ci jakaś wartośc, ja mam np sin β= | to jest to 0.6666 czyli 42o z tablic | |
| 3 |
| a | b | ||
= | |||
| sinα | sinβ |
| 2 | ||
sinβ= | ... a skoro β może przyjmować wartości 0o<β<150o ... to chyba jasne −  | |
| 3 |
 . Teraz rozumiem, wzory redukcyjne ... .
. Teraz rozumiem, wzory redukcyjne ... .
