g analityczna
zd: W trojkacie ABC dane sa A(2,−2) B(−6,6). Wiadomo ponadto ze pole trojkata jest rowne 16 oraz
kat przy wierzcholku C jest prosty. Wyznacz wspolrzedne C.
18 lip 15:27
zd: pomoze ktos?
18 lip 16:24
Święty: 1) Narysuj rysunek
2) Znajdz długość odcinka |AB|
3) Wiedząc, że kąt przy wierzchołku C jest prosty i znając pole trójkąta znajdź długość
przyprostokątnej
4) Znajdź równanie prostej AB
5) Korzystając z warunku prostopadłości znajdź równanie przyprostokątnej
6) Punkt C będzie miał współrzędne (x
c, równanie przyprostokątnej), więc z długości boku AC
będziesz w stanie podać jego dokładne współrzędne.
Może można prościej i szybciej to rozwiązać

18 lip 16:43
AS: Przyjmij C(x,y) i wykorzystaj
1 . Tw. Pitagorasa AC2 + BC2 = AB2
2. Wzór na pole trójkąta prostokątnego: 1/2*AC*BC =− 16
Rozwiąż układ równań
18 lip 16:43
pigor: ...wierzchołek
C=(x,y)=? leży na okręgu o średnicy AB i równaniu
(x+2)2+(y−2)2=16*2, oraz spełnia równanie pola ΔABC
[(x−2)2+(y+2)2]*[(x+6)2+(y−6)2]=162 i z tego układu widać, że istnieją 4 rozwiązania
(wierzchołki C) , czyli trójkąt prostokątne spełniające warunki zadania i teraz cały problem
polega na umiejętnym (jakby to zrobić, ale się nie narobić

) rozwiązaniu tego układu,
na co ja na razie pomysłu, a więc i ochoty nie mam ...

18 lip 17:17
Mila: II sposób:
(x+2)2+(y−2)2=32 równanie okręgu.
PΔ=O,5 |AB|*h
|AB|=√((−6−2)2+(6+2)2=√128=8√2
16=0,5*8√2*h
h=2√2
C leży na okręgu w odległości 2√2 od prostej AB.
Prosta AB:
y=ax+b
2a+b=−2
−6a+b=6 rozwiąż.
a=−1
b=0
stąd
y=−x
x+y=0 postać ogólna
prosta k równoległa do AB i przechodząca przez punkt C(x,y) ma równanie
k: y=−x+b
x+y−b=0 postać ogólna równania
odległość między tymi prostymi wynosi 2√2
2√2=U{|b−0|}{√12+12
|b|=4
b=4 lub b=−4
y=−x+4
lub y=−x−4
podstaw do równania okręgu i otrzymasz rozwiązania.
Jeśli będą pytania to jestem jeszcze chwilę, a potem po 22.
18 lip 17:55
Gustlik:
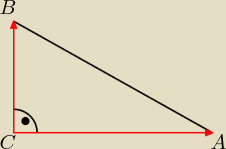
W trojkacie ABC dane sa A(2,−2) B(−6,6). Wiadomo ponadto ze pole trojkata jest rowne 16 oraz
kat przy wierzcholku C jest prosty. Wyznacz wspolrzedne C.
Znowu zadanie, które przy pomocy wektorów (których nie ma w programie na podstawach) jest do
zrobienia PIORUNEM

!
Wykorzystaj informacje o polu trójkąta:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18
i o iloczynie skalarnym wektorów − wzór:
https://matematykaszkolna.pl/strona/1629.html oraz prostopadłość wektorów:
https://matematykaszkolna.pl/strona/1630.html .
A(2,−2)
B(−6,6)
C(x, y)
Liczę wspołrzędne wektorów CB
→ i CA
→
CB
→=[−6−x, 6−y]
CA
→=[2−x, −2−y]
Liczę wyznacznik tych wektorów − będzie potrzebny do pola:
d(CB
→, CA
→)=
|−6−x 6−y|
|2−x −2−y|
=(−6−x)(−2−y)−(6−y)(2−x)
| | 1 | | 1 | |
P= |
| |d(CB→, CA→)|= |
| |(−6−x)(−2−y)−(6−y)(2−x)| |
| | 2 | | 2 | |
Liczę teraz iloczyn skalarny tych wektorów − będzie potrzebny do zbadania ich prostopadłości:
CB
→*CA
→=(−6−x)(2−x)+(6−y)(−2−y)
Otrzymuję układ równań:
| | 1 | |
{ |
| |(−6−x)(−2−y)−(6−y)(2−x)|=16 (z pola) |
| | 2 | |
{ (−6−x)(2−x)+(6−y)(−2−y)=0 (iloczyn skalarny=0 − warunek prostopadłości
wektorów)
| | 1 | |
{ |
| |(−6−x)(−2−y)−(6−y)(2−x)|=16 /*2 |
| | 2 | |
{ (−6−x)(2−x)+(6−y)(−2−y)=0
{ |(−6−x)(−2−y)−(6−y)(2−x)|=32
{ (−6−x)(2−x)+(6−y)(−2−y)=0
Otrzymujesz dwa przypadki:
1
o
{ (−6−x)(−2−y)−(6−y)(2−x)=32
{ (−6−x)(2−x)+(6−y)(−2−y)=0
lub
2
o
{ (−6−x)(−2−y)−(6−y)(2−x)=−32
{ (−6−x)(2−x)+(6−y)(−2−y)=0
Rozwiąż teraz te układy równań − najprawdopodobniej po wymnożeniu nawiasów wyjdą proste r
ównania, bo robiłem tego typu zadania..
18 lip 23:40
zd: x+y−b=0 postać ogólna równania
odległość między tymi prostymi wynosi 2√2
2√2=U{|b−0|}{√12+12
i dlaczego tam jest b−0?
19 lip 11:42
Mila: Prosta AB ma równanie ogólne;x+y=0 czyli C=0 (Ax+By+C=0)
prosta k: x+y−b=0 postać ogólna równania
| | |C1−C2| | |
2√2= |
| odległość między prostymi równoległymi |
| | √A2+B2 | |
C
1=−b
C
2=0
19 lip 15:46

 ) rozwiązaniu tego układu,
na co ja na razie pomysłu, a więc i ochoty nie mam ...
) rozwiązaniu tego układu,
na co ja na razie pomysłu, a więc i ochoty nie mam ... 
 W trojkacie ABC dane sa A(2,−2) B(−6,6). Wiadomo ponadto ze pole trojkata jest rowne 16 oraz
kat przy wierzcholku C jest prosty. Wyznacz wspolrzedne C.
Znowu zadanie, które przy pomocy wektorów (których nie ma w programie na podstawach) jest do
zrobienia PIORUNEM
W trojkacie ABC dane sa A(2,−2) B(−6,6). Wiadomo ponadto ze pole trojkata jest rowne 16 oraz
kat przy wierzcholku C jest prosty. Wyznacz wspolrzedne C.
Znowu zadanie, które przy pomocy wektorów (których nie ma w programie na podstawach) jest do
zrobienia PIORUNEM  !
Wykorzystaj informacje o polu trójkąta: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18
i o iloczynie skalarnym wektorów − wzór: https://matematykaszkolna.pl/strona/1629.html oraz prostopadłość wektorów: https://matematykaszkolna.pl/strona/1630.html .
A(2,−2)
B(−6,6)
C(x, y)
Liczę wspołrzędne wektorów CB→ i CA→
CB→=[−6−x, 6−y]
CA→=[2−x, −2−y]
Liczę wyznacznik tych wektorów − będzie potrzebny do pola:
d(CB→, CA→)=
|−6−x 6−y|
|2−x −2−y|
=(−6−x)(−2−y)−(6−y)(2−x)
!
Wykorzystaj informacje o polu trójkąta: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18
i o iloczynie skalarnym wektorów − wzór: https://matematykaszkolna.pl/strona/1629.html oraz prostopadłość wektorów: https://matematykaszkolna.pl/strona/1630.html .
A(2,−2)
B(−6,6)
C(x, y)
Liczę wspołrzędne wektorów CB→ i CA→
CB→=[−6−x, 6−y]
CA→=[2−x, −2−y]
Liczę wyznacznik tych wektorów − będzie potrzebny do pola:
d(CB→, CA→)=
|−6−x 6−y|
|2−x −2−y|
=(−6−x)(−2−y)−(6−y)(2−x)