rysowanie wykresów funkcji bartekcmg: Naszkicuj wykresy funkcji: 1) f(x)=x²/3 2) f(x)=arctgx/3 3) f(x)=2arctg3x 4) f(x)=1/2+lnx Bardzo proszę o wskazówki...

Mila: 1) Częściowa tabelka wartości ( pamiętaj o dziedzinie) 2) szkic 3) sprawdzenie − wolfram alpha

picia:

	1
hmm...mnie sie zdaje ze 1) to		x2 i dziedzina sa wszystkie liczby rzeczywiste
	3

Mila: Picia , a 4?

bartekcmg: w tym 1) jest x do potęgi 2/3 ... sorki za pomyłkę

bartekcmg: więc w 1) zrobiłem tabelkę wartości i obliczam je z wzoru a^1/n=√a ntego stopnia kiedy biorę np x=2, to wychodzi mi pierwiastek trzeciego stopnia z 4 . I co z tym robić? Dalej przy x=3 itd. wychodzą takie same "dziwne" liczby. nie wiem nadal jak to dalej rozwiązywać...

Saizou : zobacz co picia napisał, że jest to funkcja kwadratowa

Saizou : sorry moje nie doczytanie

Saizou : tam ma być f(x)=_x^2₃

bartekcmg: ma ktoś jakiś pomysł?

Saizou : _x^2₃= ³√x² tam jest napisane pierwiastek 3 z x² i x∊R teraz tabelka: x 1 8 −1 −8 y 1 4 −1 −4

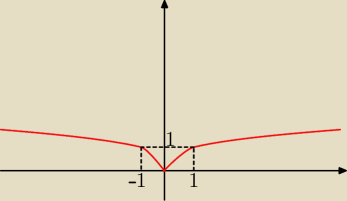
Basia: jeżeli f(x) = x^2/3 ⇒ D = R i tak jak napisała Mila; tabelka częściowa wykres wygląda mniej więcej tak jak na rysunku

Saizou : poprawka pierwiastek 3 stopnia z x²

bartekcmg: a czy lewa strona nie powinna być pod osią?

Saizou : fakt błąd w obliczeniach x 1 8 −1 −8 y 1 4 1 4

bartekcmg: a nie sorki kwadrat redukuje minusy ok dzieki za ten przykład, w złym miejscu wykorzystałem wzór na potęgowanie... a co z pozostałymi przykładami?

bartekcmg: f(x)=arctgx/3 domyślam się że wykres będzie bardzo rozciągnięty w szerokość, ale jak to konkretnie pokazać ?

Basia: będzie miał kształt taki jak wykres funkcji g(x) = arctgx i te same asymptoty

	π
y = ±
	2

tylko będzie bardziej spłaszczony

	π
wolniej będzie dążył do tych wartości ±
	2

np.

	3		π
f(3) = arctg		= arctg1 =
	3		4

	−3		π
f(−3) = arctg		= arctg(−1) = −
	3		4

g(x) = arctgx osiąga je szybciej bo dla x=±1

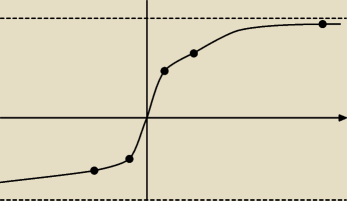
Mila: f(x)=2arctg3x zbiór wartości:

	π		π
−		<arctg3x<		/*2
	2		2

−π<2arctg3x<π asymptoty poziome y=−π i y=π≈3,14

	π		π
f(−1/3)=2*arctg(−1)=2*−		=−		≈−1,6
	4		2

	π		π
f(1/3)=2*arctg1=2*		=		≈1,6
	4		2

	π
f(−√3/3)=2*arctg(−√3)=2*−		≈ −2
	3

	π
f(√3/3)=2*arctg(√3)=2*		≈ 2
	3

f(2)=2*arctg6≈2*1,4=2,8 Naszkicowałam, ale mało dokładnie

Mila: zadanie 4)

	1
f(x)=		+lnx
	2

D: x>0 1) sporządź tabelkę dla funkcji y=lnx 2) naszkicuj wykres

	1
3) przesuń o wektor [0,		] (o pół jednostki w górę.)
	2

bartekcmg: no właśnie ta tabelka... nie wiem jak obliczać wartości dla lnx, w sensie jak to zamienić na liczbę dającą się zaznaczyć na osi... moglibyście podać przykład jak obliczyć np. dla x=1 ?

Mila: ln1 =0 lne=1 (e≈2,7) ln(1/e)=−1 lne²=2 (e²≈7,3) masz naszkicować, zatem punkty trochę mało dokładne.

bartekcmg: dzieki bardzo

Mila: