g analityczna
zd: Prosta 2x + y− 13 = 0 zawiera bok AB tr�ojka�ta ABC, prosta x − y − 5 = 0 zawiera
bok BC, a prosta 3x−y− 7 = 0 zawiera dwusieczna� ka�ta ACB. Znajd�z wierzchołki
tego tr�ojka�ta i oblicz jego pole.
12 lip 20:50
Leszek: Obliczenie współrzędnych punktu B:
2x+y−13=0
x−y−5=0
________+
3x=18
x=6
y=x−5=6−5=1
B(6,1)
Obliczenie współrzędnych punktu C:
3x−y−7=0
x−y−5=0
_______−
2x−2=0
x=1
y=x−5=−4
C(1,−4)
Obliczenie współczynników kierunkowych dwusiecznej ACB(a
1) i prostej BC(a
2)
y=3x−7 → a
1=3
y=x−5 → a
2=1
Obliczenie tangensa kąta między dwusieczną ACB i prostą BC:
Obliczenie współczynnika kierunkowego prostej AC(a
3):
2a
3−6=1+3a
3
a
3=−7
Wyznaczenie prostej AC:
−4=−7*1+b
3
b
3=3
y=−7x+3
Wyznaczenie współrzędnych punktu A:
y=x−5
y=−7x+3
________−
8x=8
x=1
y=1−5=−4
A(−1,−4)
Jeszcze trzeba pole policzyć...
12 lip 21:25
Leszek: sorry A ma (1,−4)
12 lip 21:25
Leszek:
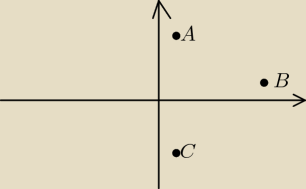
Długość podstawy AC:
a=|AC|=4−(−4)=8
Wysokość opuszczona z B
h=6−1=5
Pole
A=0.5*a*h=20 j
2
12 lip 21:30
Leszek: Pomyłka przy znajdowaniu punktu A ,jeszcze raz:
y=−2+13
y=−7x+3
________−
5x=−10
x=−2
y=(−2)*(−2)+13=17
A(−2,17)
12 lip 21:43
Leszek:
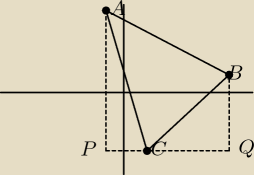
Pole trapezu APQB:
A
1 = 0.5*(17−(−4)+1−(−4))*6−(−2)=0.5*(21+5)*6=78
Pole trójkąta APC:
A
2 = 0.5*21*(1−(−2))=31,5
Pole trójkąta BQC:
A
3 = 0.5*5*(6−1)=12,5
Polec trójkąta ABC:
A=A
1−(A
2+A
3)=34 j
2
12 lip 21:55
pigor: ...
PΔABC=12(5+21)*8−
12*3*31−
125
2=4*26−
12(63+25)=104−44=
60 j2
12 lip 23:23
Gustlik:
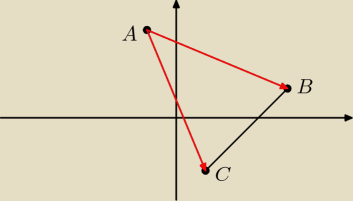
Obliczę pole najprostszym sposobem − skorzystam z obliczeń
Leszka
A=(−2,17)
B=(6,1)
C=(1,−4)
Z wektorów:
AB
→=[6−(−2), 1−17]=[8, −16]
AC
→=[1−(−2), −4−17]=[3, −21]
Wyznacznik wektorów:
d(AB
→, AC
→)=
| 8 −16 |
| 3 −21 |
=8*(−21)−(−16)*3=−168+48=−120
| | 1 | | 1 | |
Odp: P= |
| |d(AB→, AC→)|= |
| *|−120|=60 |
| | 2 | | 2 | |
12 lip 23:48
Leszek: dobra poprawiając moje odliczenia:
Pole trapezu APQB:
A1 = 0.5*(17−(−4)+1−(−4))*6−(−2)=0.5*(21+5)*8=104
A=A1−(A2+A3)=60 j2
Dzięki że sprawdzacie mnie bo czasami coś pomijam...
13 lip 00:12
pigor: ... no to może policzę inaczej (bez kąta ) wierzchołek
A=(x,y)=? np.
tak :
niech [n[B'] − obraz punktu B=(6,1) w symetrii względem danej dwusiecznej 3x−y−7=0, to
prosta BB'⊥ do niej : x+3y+C=0 i 6+3*1+C=0 ⇒ C=−9 , czyli
BB': x+3y−9=0 przecina
ją w punkcie S − środku odcinka BB' takim, że 3x−y−7=0 i x+3y−9=0 ⇔ x+3y=9 i
9x−3y=21 /+ stronami ⇔ 10x=30 i y=3x−7 ⇔
S=(3,2) , zatem
jeśli
B'=(x,y), S=(3,20) , B=(6,1) , to x+6=2*3 i y+1=2*2 ⇔
B'=(0,3), a
ponieważ
C=(1−4) , więc prosta CB': y+4=
3+40−1(x−1) ⇔ y+4=−7x+7 , czyli
CB': 7x+y−3=0 , a
wtedy punkt A: to punkt przecięcia się prostych BA i CB' : 2x+y−13=0 i 7x+y−3=0 /−
stronami ⇔ 5x=−10 i y=13−2x ⇔ x=−2 i y=17 , czyli
A=(−2,17) − szukany 3−ci
wierzchołek ΔABC ,
−−−−−−−−−−−−−
| 1 6 1 |
i na koniec P
Δ=
12| | 1 1 −4 | | =
12 |17−24−2−1−8−102|=
12*120=
60j
2.

| 1 −2 17 |
13 lip 10:48
 Długość podstawy AC:
a=|AC|=4−(−4)=8
Wysokość opuszczona z B
h=6−1=5
Pole
A=0.5*a*h=20 j2
Długość podstawy AC:
a=|AC|=4−(−4)=8
Wysokość opuszczona z B
h=6−1=5
Pole
A=0.5*a*h=20 j2
 Pole trapezu APQB:
A1 = 0.5*(17−(−4)+1−(−4))*6−(−2)=0.5*(21+5)*6=78
Pole trójkąta APC:
A2 = 0.5*21*(1−(−2))=31,5
Pole trójkąta BQC:
A3 = 0.5*5*(6−1)=12,5
Polec trójkąta ABC:
A=A1−(A2+A3)=34 j2
Pole trapezu APQB:
A1 = 0.5*(17−(−4)+1−(−4))*6−(−2)=0.5*(21+5)*6=78
Pole trójkąta APC:
A2 = 0.5*21*(1−(−2))=31,5
Pole trójkąta BQC:
A3 = 0.5*5*(6−1)=12,5
Polec trójkąta ABC:
A=A1−(A2+A3)=34 j2

 Obliczę pole najprostszym sposobem − skorzystam z obliczeń Leszka
A=(−2,17)
B=(6,1)
C=(1,−4)
Z wektorów:
AB→=[6−(−2), 1−17]=[8, −16]
AC→=[1−(−2), −4−17]=[3, −21]
Wyznacznik wektorów:
d(AB→, AC→)=
| 8 −16 |
| 3 −21 |
=8*(−21)−(−16)*3=−168+48=−120
Obliczę pole najprostszym sposobem − skorzystam z obliczeń Leszka
A=(−2,17)
B=(6,1)
C=(1,−4)
Z wektorów:
AB→=[6−(−2), 1−17]=[8, −16]
AC→=[1−(−2), −4−17]=[3, −21]
Wyznacznik wektorów:
d(AB→, AC→)=
| 8 −16 |
| 3 −21 |
=8*(−21)−(−16)*3=−168+48=−120
 | 1 −2 17 |
| 1 −2 17 |