Naszkicuj wykres funkcji fhrh: f(x)=|x²−4|−4

	⎧	x2−4−4 ,gdy x≥0 ⇒ x2−8
f(x)=	⎨
	⎩	−x2−4−4 , gdy x<0 ⇒ −x2−8

Jaka jest metoda rozwiązywania takich zadań? Próbowałem przez delte i liczenie współrzędnych wierzchołka ale jakoś słabo to idzie, ponieważ rozwiązanie nie pokrywa się z tym z zbioru.

Beti: błędnie rozpisałeś wzór tej funkcji. Powinno być tak: x²−4−4 , gdy x²−4 ≥ 0 f(x) = −x²+4−4 , gdy x²−4 < 0 czyli: x²−8 , gdy x∊(−∞,−2> ∪ <2,∞) f(x) = −x² , gdy x∊(−2,2)

Beti: A wogóle, to najszybciej narysujesz, jeśli wykorzystasz przekształcenia wykresu funkcji podstawowej, czyli y = x²

Saizou : Beti najszybciej nie znaczy najdokładniej

Artur z miasta Neptuna: odnośnie rysunków: http://www.wolframalpha.com/input/?i=plot+%5Bx%5E2%3B+x%5E2-4%3B+abs%28x%5E2-4%29%3B+abs%28x%5E2-4%29+-+4%5D+from+-4+to+4

Artur z miasta Neptuna: odnośnie rysunków: http://www.wolframalpha.com/input/?i=plot+%5Bx%5E2%3B+x%5E2-4%3B+abs%28x%5E2-4%29%3B+abs%28x%5E2-4%29+-+4%5D+from+-4+to+4

Artur z miasta Neptuna: odnośnie rysunków: http://www.wolframalpha.com/input/?i=plot+[x^2;+x^2-4;+abs(x^2-4);+abs(x^2-4)+-+4]+from+-4+to+4

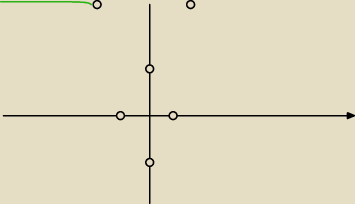
Mila: 1) rysuję wykres y=x²−4 x₁=−2 , x₂=2 (0,−4) współrzędne wierzchołka paraboli.

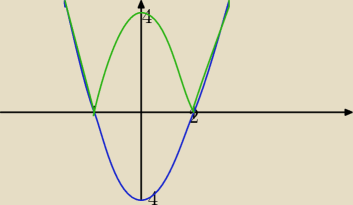
Mila: No i nic nie wyszło.Spróbuję jeszcze raz.

Mila: Zielony wykres( szkic) to y=|x²−4|, teraz należy przesunąć go o wektor [0,−4] ( czyli 4 jednostki w dół). Komentarz pod ostatnim rysunkiem dotyczy postu z 19⁰².

Beti: Saizou, pisząc "najszybciej" miałam na myśli dokładnie i szybko (zwłaszcza jak się dysponuje szablonami podstawowych paraboli)

Saizou : Beti na początki trzeba mieć te szablony, których nie posiadam

Eta: Hehe Kiedyś moi uczniowie mieli takie szablony wycięte z pleksy

Saizou : może się w taki zaopatrzę ale to w roku szkolnym

Trivial: Zdecydowanie najszybciej jest ręcznie.

Eta: Chyba odręcznie

Saizou : według mnie najszybciej wbić wzór do geogebry i gotowe

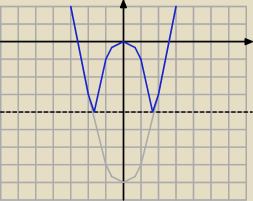
Bogdan: Najpierw narysowałem prostą y = −4 i potraktowałem te prostą tak, jakby była osią x (mówiąc inaczej, przesunąłem układ współrzędnych o 4 jednostki w dół). Na tym "nowym" układzie współrzędnych narysowałem wykres y = x² − 4 (na oryginalnym układzie ten wykres miałby wzór y = x² − 8), część wykresu znajdującą się pod prostą (linia przerywana) pełniącą rolę nowej osi x przeniosłem na drugą stronę tej prostej.