Do Basi
Gustlik: Do
Basi, zwolenniczki "logicznego myślenia":
Droga
Basiu, tak się ze mną sprzeczasz, a co powiesz na takie zadanie?
Oblicz pole trójkąta o wierzchołkach A=(1, 1), B=(2, 2), C=(3, 9)
Zakładamy, że nauczyciel trzyma się ściśle podstawy programowej, nie ma mowy więc o wektorach,
a nawet o wzorze na odległość punktu od prostej.
| | 1 | |
Wtedy uczeń musi zastosować klasyczny wzór P= |
| ah |
| | 2 | |
I procedura jest taka:
1. Liczymy długość podstawy a=|AB| ze wzoru:
https://matematykaszkolna.pl/strona/1248.html ,
2. Wyznaczamy równanie prostej AB, nazwijmy ja prostą a ze wzoru
https://matematykaszkolna.pl/strona/1223.html lub układem równań, a
więc dwiema najbardziej skomplikowanymi metodami,
3. Z warunku prostopadłości wyznaczamy równanie wysokości trójkąta opuszczonej z wierzchołka C,
nazwijmy ją prostą h,
4. Wyznaczamy współrzędne punktu D bedącego spodkiem wysokosci rozwiązując układ równań
prostych a i h,
5. Obliczamy wysokość h jako długość |CD| tym samym wzorem co bok |AB|
6. Podstawiamy a i h do wzoru na pole i liczymy je.
Zadanie można nieco uprościć, jeżeli zna się wzór na odległość punktu od prostej, bo tym wzorem
można obliczyć wysokość, wtedy omijamy pkt. 3, 4 i 5. Ale i tak zadanie jest dość
skomplikowane.
A co będzie, jak trzeba obliczyć pole czworokąta? Wtedy 2 razy taka żmudna procedura, bo trzeba
figurę podzielić przekątną na 2 trójkaty i liczyć 2 razy pole.
Tyle samo, co obliczenie pola trójkąta taką skomplikowaną metodą, zajmie nauczycielowi
wytłumaczenie uczniom, jak się oblicza współrzędne wektorów i wyznaczniki, bo to jest proste
jak konstrukcja młotka, potem co to jest iloczyn wektorowy, jak się go oblicza z długości
wektorów i kąta oraz ze współrzędnych i wyprowadzenie wzoru na pole trójkąta
| | 1 | | 1 | | 1 | |
P= |
| ah= |
| absinα=...= |
| |d(AB→, AC→)|, zwłaszcza, że nauczyciel to zrobi tylko |
| | 2 | | 2 | | 2 | |
raz, a jak znamy ten wzór to procedura jest banalna:
1. Liczymy współrzędne wektorów AB
→ i AC
→ ze wzoru
https://matematykaszkolna.pl/strona/1623.html ,
2. Liczymy wyznacznik wektorów d(AB
→, AC
→) ze wzoru
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 ,
| | 1 | |
3. Liczymy pole trójkąta ze wzoru P= |
| |d(AB→, AC→)|. |
| | 2 | |
To sie wtedy robi w 3, góra 4 linijkach i trwa to kilka sekund.
I wtedy pole czworokąta też nie jest straszne.
Co
Basiu powiesz na to

?
10 lip 15:50
rumpek: W podstawie programowej jest wzór:
| | 1 | |
P = |
| | (xB − xA)(yC − yA) − (yB − yA)(xC − xA) | |
| | 2 | |
To w sam raz dla trójkąta, a dla czworokąta to dzielimy na dwa trójkąty i sumujemy pola

2
linijki

P.S. Tak wiem nie jestem
Basią 
10 lip 16:06
Artur_z_miasta_Neptuna:
Gustlik −−− wybacz ... ale nie jestem w stanie zaakceptować, że 17 latek zrozumie (pojmie o co
chodzi) co to jest wyznacznik
iloczyn wektorowy −−− w 99% procentach wbije na pamięć wzór.
To wszystko śliczne i piękne pod warunkiem że ZNASZ WZORY



Sam wielokrotnie pisałeś, ze
matura to stres −−− no to co pocznie biedny (słaby) maturzysta który nagle zapomni jak się
liczyło wyznacznik? Panika ... gryzienie pazurów ... załamanie nerwowe ... itd. itp.
A człek mało inteligentny (bo taki nie zdał matury podstawowej) tychże wzorów znać nie będzie

Pomijając całą resztę wzorów, które byłyby pomocne w 'szybszym' zrobieniu innych zadań.
Gustlik −−− metoda wektorowa jest cudowna pod warunkiem, że się wie (i pamięta) co to jest
iloczyn wektorowy i jak się wylicza wyznacznik macierzy 3x3 −−− a z tym ma problemy minimum
~50% studentów kierunków technicznych bądź finansowych.
Dlatego też nie rozumiem dlaczego chcesz nam na siłę (poniekąd) wmówić, że gdyby 'krótsze'
metody były stosowane przez WSZYSTKICH nauczycieli to zdawalność matury byłaby większa.
Gustlik −−− ile uczni za Twoich czasów zdawało maturę (jaki procent kończących średnią szkołę
podchodziło do matury i ją zdawało)
A ile jest obecnie? Czy procent 'inteligentnych' uczniów się zwiększył? Nie ... więc niby
dlaczego teraz ma dojśc do tego, że 100% uczniów kończących szkołę średnią ma zdać maturę?
A co do pola czworokąta −−− mam nadzieję, ze nie mówisz o polu dowolnego czworokąta, bo jeżeli
tak to wybacz ale śmiem się nie zgodzić.
10 lip 16:07
Krzysiek: A co powiesz na metodę: 'z rysunku'? wtedy rozwiązanie jest natychmiastowe...(wystarczy znać
długość przekątnej kwadratu o boku 1 )
10 lip 16:09
rumpek: Ale
Baś mamy na forum

10 lip 16:10
pigor: ...

no to może jeszcze coś takiego dla chętnych :
| 1 x
A y
A |
P
Δ=
12* | | 1 x
B y
B | | ,
| 1 x
C y
C |
10 lip 16:59
Trivial: Wzór Herona jest na podstawie?
10 lip 17:37
rumpek: Tak

10 lip 17:45
Mila: Oblicz pole trójkąta o wierzchołkach A=(1, 1), B=(2, 2), C=(3, 9)
Takie zadanie rozwiązuje uczeń klasy 6, bez znajomości "niczego" z powyższych mądrości.
Umie zaznaczyć punkty i umie obliczyc pole prostokata oraz pole Δ prostokątnego.
Pozdrawiam dyskutantów.
Rumpek, jesteś specjalistą od zadań z prawdopodobieństwa, zobacz proszę zadanie u W18*.
I w ogóle, to jakie studia wbrałeś, i kto Ciebie wybrał?
10 lip 18:08
rumpek: Postawiłem na Informatykę, tam gdzie złożyłem tam się dostałem (Poznań, Wrocław, Warszawa)
teraz tylko wybrać uczelnie

. (mój cichy pretendent to Poznań). No nic do 16 mam czas

.
10 lip 19:22
AS:
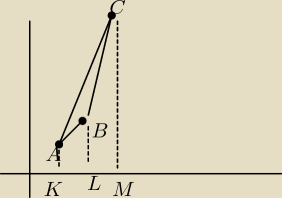
Zastosować metodę trapezów
1. Trapez KACM
| | 1 | | 1 | |
P1 = |
| *(AK + MC)*KM = |
| *(1 + 9)*(3 − 1) = 10 j2 |
| | 2 | | 2 | |
2. Trapez KABL
| | 1 | | 1 | |
P2 = |
| *(AK + BL)*KL = |
| *(2 + 3)*(2 − 1) = 5/2 = 2.5 j2 |
| | 2 | | 2 | |
3. Trapez LBCM
| | 1 | | 1 | |
P3 = |
| *(LB + MC)*LM = |
| *(2 + 9)*(3 − 2) = 11/2 = 5.5 j2 |
| | 2 | | 2 | |
Szukane pole:
P = P1 − P2 − P3 = 10 − 2.5 − 5.5 = 10 − 8 = 2 j
2
10 lip 20:23
Leszek: Metodą jaką przedstawił AS każdy gimnazjalista może łatwo obliczyć pole każdego wielokąta a
Gustlik potrzebuje wyznaczników do tego.
10 lip 21:04
Eta:
Nasz
Gustlik jest zakochany w wektorach

10 lip 21:19
AS: Dodam jeszcze uwagę,gdyby któryś z wierzchołków leżał
poniżej osi Ox , należy przesunąć cały wielokąt w górę o tyle
jednostek,by wszystkie wierzchołki wielokąta leżały powyżej osi Ox.
10 lip 21:22
Trivial:
Eto, stąpasz po cienkim lodzie. Właśnie tym jednym krótkim wpisem naraziłaś się na full
wykład o wyższości wektorów nad dowolnie wybraną inną abstrakcją matematyczną.
10 lip 21:38
Leszek: Można też dać te punkty K L M bezpośrednio pod trójkątem czyli K pokrywa się z A i mamy 2
trójkąty i 1 trapez zamiast 3−ech, jak się rysuje na kartce w kratkę to można łatwo policzyć
kratki albo można odjąć.
10 lip 21:38
Godzio:
A ja się w tym momencie w pełni zgodzę z
rumpkiem, jest wzór to trzeba korzystać

W
karcie wzorów również jest, więc nie widzę problemu

10 lip 21:40
Eta:

10 lip 21:43
Eta:
Dzięki
Trivial 
Właśnie mi przypomniałeś! ( lody w zamrażarce czekają ... "Magnum almond"

Co ja bym bez Ciebie zrobiła

10 lip 21:47
Trivial: Prawdopodobnie egzystowałabyś w nieświadomości.

10 lip 21:49
Godzio: Dzięki
Eta, właśnie wziąłem rożka truskawkowego

10 lip 21:49
Eta:

10 lip 21:51
Vax: I tak najlepszy wzór Picka


10 lip 21:53
Trivial: Ah.. Vax i jego tricki...
10 lip 21:55
Saizou : Vax właśnie chciałem pokazać ten sposób
10 lip 21:55
Eta:
Tricek Picka

10 lip 21:56
10 lip 21:57
Eta:
Właśnie , pole też mi wychodzi 3 [j
2] , a
AS podał,że
2 
10 lip 22:00
Vax: Tylko mała literówka, punkty
kratowe 
10 lip 22:03
10 lip 22:13
Saizou : Vax wakacje są, a ten wzór miałem bodajże w pierwszej gimnazjum
10 lip 22:14
Mila: Rumpek, gratuluję.
Vax znowu wzór? Ile razy wprowadzałam, starczyło na chwilę.
Leszek, to zadanie dla podstawówki.
Eta , smacznego. Niestety mam nadwagę i jem mrożony mus truskawkowy.
Saizou

.
10 lip 22:21
Saizou : Dziękuję Mila ale to zadanie nie wykracza za poziom podstawówki
10 lip 22:25
ZKS:
To ja dodam wzór jaki zapamiętałem z Geodezji

x
n | y
n | y
n + 1 − y
n − 1 | x
n(y
n + 1 − y
n − 1)
1 1 −7 −7
2 2 8 16
3 9 −1 −3
2P = −7 + 16 − 3 ⇒ P = 3
10 lip 22:35
Leszek: może i jest to zadanie dla podstawówki ale obecnie na maturze są łatwiejsze rzeczy

10 lip 22:43
Mila: Saizou, chodzi mi właśnie o sposób dostosowany do podstawówki.
10 lip 22:57
pigor: ... no to zobaczę co też wyjdzie z "mojego" wyznacznika :
PΔ=12|18+2+3−2−6−9|=
12|20−14|=
3 j
2 . ...

10 lip 23:43
Gustlik: Rumpek, ten Twój wzór to właśnie wywodzi się z wyznacznika wektorów:
d(d(AB
→, AC
→)=
| x
B−x
A y
B−y
A |
| x
C−x
A y
C−y
A |
=(x
B−x
A)(y
C−y
A)−(y
B−y
A)(x
C−x
A)
| | 1 | | 1 | |
P= |
| |d(AB→, AC→)|= |
| |(xB−xA)(yC−yA)−(yB−yA)(xC−xA)| |
| | 2 | | 2 | |
Tylko w takiej formie jest o wiele cieżej strawny. De facto robisz to samo, co ja, tylko na
ogólnych danych i długim tasiemcowym wzorem.
Powiem szczerze: ja tego wzoru w tej postaci na pamięć nie znam. Gdybym chciał nim robić,
musiałbym sobie za każdym razem robić takie wyprowadzenie jak powyżej albo tracić czas na
szukanie w tablicach. Tylko po co, jak wektorami jest przejrzyściej? I tym sposobem zrobię to
samo, tylko w 3 linijki, szybko i sprawnie. I tak nauczam uczniów i wolą te metodę od
szkolnej.
A wyznacznikiem robisz szybko, w górnym wierszu współrzędne AB
→, w dolnym AC
→, na krzyż I
przekątna minus II przekątna i po sprawie.
ArturzmiastaNeptuna Co do tego, że 17−latek nie zrozumie wyznaczników − mylisz się.
Gimnazjalistów uczę rozwiązywania wyznacznikami układów równań i rozumieją, co to wyznacznik i
jak się go liczy. I wolą metodę wyznacznikową od podstawiania czy nawet przeciwnych
współczynników.
Ponadto do czego Ci wyznacznik 3x3? Chyba że liczysz pole trójkąta w przestrzeni, a o ile sie
nie mylę, w LO nie ma geometrii analitycznej w przestrzeni, nawet na rozszerzeniu.
Owszem, można wzorem
Pigora, ale mało kto zna ten wzór. Wtedy faktycznie trzeba byłoby
pokazać metodę Sarrusa na wyznaczniki 3x3. Tylko czy jest taka potrzeba? Wyznacznik wektorów
to wyznacznik 2x2 i taki w zupełności wystarczy..
Eta, ja jestem zakochany nie tylko w wektorach, ale w każdej szybkiej i prostej metodzie,
m.in . w schemacie Hornera, w obliczaniu ciągów liczbowych równaniami z jedną niewiadomą, a
nie układem, a jestem wrogiem krętych ścieżek, bo uczeń się potem myli, robi długo i traci
czas. Co jest trudnego w wektorach? Odjąć współrzędne początku od współrzędnych końca? Nie
wiem, czemu to jest na rozszerzeniu, 6−klasista to zrobi. Ktoś mi kiedyś tu przypisał hasło
"śmierć krętym ścieżkom". W dużej części to prawda, choć ja te ścieżki pokazuję, a potem
pokazuję proste i dalej jedziemy prostymi.
10 lip 23:51
Gustlik: Leszek owszem dobra metoda dla gimnazjalistów, ale ogólnie dłuższa. Wektorami jest
szybciej, wzłaszcza, że metoda wektorowa jest banalnie prosta. Ja całą geometrię analityczną w
LO uczę wektorami, od równania prostej po pola figur, bo jest dużo łatwiej. Ponadto często się
zdarza, że w zadaniu masz kilka podpunktów, np. a) wyznacz równanie prostej AB, b) wyznacz
równanie wysokości trójkąta opuszczonej z pkt C, c) oblicz pole trójkąta. Wtedy raz obliczone
współrzędne wektora AB
→ w pkt. a) można wykorzystać do pkt. b) i c), bez wektorów trzeba
wszystko liczyć od zera. Nie wiem czemu wektory poszły na rozszerzenie, skoro są proste i
wielu uczniów je rozumie i woli nimi robić, a zadania na dowodzenie zostały na podstawie,
podczas gdy większość uczniów jak widzi w poleceniu "wykaż, że" to dostaje co najmniej stanu
przedzawałowego.
Takie zadania jak np. to:
https://matematykaszkolna.pl/strona/3305.html lub to:
https://matematykaszkolna.pl/strona/3307.html umieją rozwiązywać tylko uczniowie z mat−fizu,
uczniowie z podstaw bezradnie rozkładają ręce. Ja muszę im te zadania rozwiązać od A do Z, bo
sami nie ruszą. Co z tego, ze rozwiążę im i zrozumieją, a na maturze będzie inny dowód? Nawet
jedna z nauczycielek u mnie w mieście doradzała uczniom, żeby te zadania odkładali na koniec,
zwłaszcza, że są trudne, a − chyba na szczęście − nisko punktowane, bo po 2 pkt. Tyle samo
punktów dostaje się np. za nierówność kwadratową, gdzie deltę, x
1 i x
2 każby ma obcykane, a
za stosunkowo łatwe zadanie z ciągiem liczbowym:
https://matematykaszkolna.pl/strona/3389.html można było zarobić aż 4 pkt. Dziwne to,
ale tak jest.
Wg mnie jeżeli już coś musiało zniknąć z podstaw, to prędzej dowody powinny zniknąć z matury
podstawowej, bo tego prawie nikt nie umie robić, niż wektory − PODSTAWA geometrii
analitycznej, schemat Hornera − UŁATWIA rozkład wielu wielomianów na czynniki i jest lepiej
rozumiany niż np. grupowanie wyrazów, czy kombinatoryka − PODSTAWA rachunku
prawdopodobieństwa.
11 lip 00:17
Vax: A co powiesz o wzorze Picka ? Zdecydowanie szybszy niż wektory, liczysz tylko ilość punktów
kratowych.
,,Wg mnie jeżeli już coś musiało zniknąć z podstaw, to prędzej dowody powinny zniknąć z matury
podstawowej, bo tego prawie nikt nie umie robić"
Z tym to się kompletnie nie mogę zgodzić. Dowód, to jest rzecz NAJWAŻNIEJSZA w matematyce.
To, czego aktualnie uczą w gimnazjach, liceach matematyką ciężko nazwać, prędzej rachunkami...
Moim zdaniem właśnie na maturze podstawowej powinno być zdecydowanie więcej dowodów, a to, że
prawie nikt ich ,,nie umie robić" nie jest żadnym argumentem. Nie może być tak, że poziom
nauczania dostosowuje się do poziomu uczniów... Cały problem z matematyką wśród tak wielu
uczniów bierze się stąd, że już od najmłodszych lat wpaja im się wzory, reguły bez żadnego
tłumaczenia, potem wystarczy najdrobniejsza zmiana treści zadania etc i już większość osób się
gubi, gdyż nie wie pod jaki schemat to podpiąć. Aby temu zaradzić już od podstawówki powinno
się tłumaczyć, skąd się biorą te wszystkie wzory, twierdzenia i dążyć do tego, aby uczniowie
to naprawdę rozumieli. Wtedy dowody nie będą stanowiły już takiej przeszkody jak teraz, gdzie
są jedyną rzeczą, której nie da się podpiąć pod schemat i trzeba minimalnie pomyśleć...
11 lip 00:39
Gustlik:
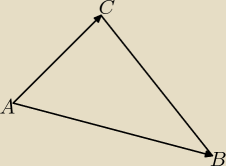 Vax
Vax, Znam wzór Picka. Ale wtedy trzeba wykonać dokładny rysunek, zliczyć punkty kratowe,
zarówno wewnętrzne jak i te na obwodzie, co przy niewielkiej nawet niedokładności może
generować błędy. Niektóre z tych punktów mogą się znaleźć bardzo blisko któregoś z boków
figury i przy niewielkiej nawet niedokładności mogą zostać uznane przez ucznia za punkty na
obwodzie figury, podczas gdy faktycznie leżą one na zewnątrz albo wewątrz figury i już jest
błąd. Albo punkty leżące na zewnątrz figury mogą się znaleźć wewnątrz niej.
Natomiast metoda wektorowa nie wymaga nawet rysunku lub co najwyżej rysunek poglądowy, jak np.
ten powyżej:
11 lip 00:47
Gustlik: Vax co do dowodów − masz rację, że powinny zostać i masz rację, że się ich prawie nie
uczy. Napisałem "Wg mnie jeżeli już coś musiało zniknąć z podstaw, to prędzej dowody
powinny zniknąć z matury
podstawowej, bo tego prawie nikt nie umie robić, niż wektory − PODSTAWA geometrii
analitycznej, schemat Hornera − UŁATWIA rozkład wielu wielomianów na czynniki i jest lepiej
rozumiany niż np. grupowanie wyrazów, czy kombinatoryka − PODSTAWA rachunku
prawdopodobieństwa.", co nie oznacza, że powinny zniknąć. Zwróć uwagę na słowo prędzej.
Dlaczego tak napisałem? Bo chciałem zaznaczyć, że skoro pozostawiono tak trudne zagadnienia,
jak dowody, to powinny zostać o wiele prostsze wektory, schemat Hornera i kombinatoryka. Tak
jak dowody są NAJWAŻNIEJSZĄ rzeczą w matematyce, tak wektory są NAJWAŻNIEJSZĄ rzeczą
w geometrii analitycznej, schemat Hornera − NAJWAŻNIEJSZĄ rzeczą w wielomianach, bo wiele
wielomianów można nim rozłożyć na czynniki, a kombinatoryka − NAJWAŻNIEJSZĄ rzeczą w
rachunku prawdopodobieństwa.
11 lip 00:56
Gustlik: Vax − piszesz, że "Moim zdaniem właśnie na maturze podstawowej powinno być zdecydowanie
więcej dowodów, a to, że prawie nikt ich ,,nie umie robić" nie jest żadnym argumentem.". Wtedy
co roku oblewałoby nie 15 %, nie 21 % a ze 40 % maturzystów. Wielu osobom − przede wszystkim
humanistom, którym dowody matematyczne są najmniej potrzebne − przekreśliłoby to marzenia o
studiach np. na polonistyce czy prawie. Moim zdaniem dobrze, że są tylko dwa dowody i − choć
to dziwne, ale dobrze, że są one nisko punktowane, bo na nich tracisz tylko 4 pkt, czyli 8 %,
jak ich nie rozwiążesz.
11 lip 01:02
Vax: Trzeba sobie zadać pytanie, czy ważne jest to, aby była wysoka zdawalność matur, czy to, aby
ludzie rozumieli matematykę, gdyż obecnie niestety to równoważne nie jest.. Jakby było tak,
jak pisałem poprzednio, czyli uczniom byłoby dokładnie tłumaczone skąd się biorą wszystkie
(większość) wzorów, twierdzeń, to jestem przekonany, że nawet dając więcej dowodów na maturze
podstawowej, odsetek osób, które nie zdały matury byłby niższy. Zwróć uwagę na to, że ,,nauka
dowodów" − czyli lepiej mówiąc − nauka logicznego myślenia przydaje się we wszystkich
działach matematyki, planimetrii, geometrii analitycznej, kombinatoryce itd... Często się
zdarza, że uczniowie liczą coś dwoma sposobami (dwoma schematami) i ostatecznie dostają 2
różne wyniki i nie wiedzą które rozumowanie jest poprawne. Zamiast pomyśleć, czy dane
rozwiązanie składa się z ciągu logicznych etapów i nie zawiera błędów rachunkowych, oni
dosłownie strzelają.. Uczeń, który przy rozwiązywaniu zadań nie stara się podpinać wszystkiego
pod schemat, tylko logicznie myśli bez problemu w wielomianach zauważy, jak można szybko
pogrupować wyrazy, nie musi korzystać z takich rzeczy jak schemat Hornera i zajmuje mu to o
wiele mniej czasu! Dodatkowo jak trafi na zadanie, które wymaga znajomości pewnych wzorów a
ich pamiętać nie będzie, dzięki umiejętności logicznego myślenia będzie mógł sobie dane
zależności wyprowadzić.. Jak widać, nauka logicznego myślenia przynosi wyłącznie ogromne
plusy. Wspomniałeś również o tym, że jest wiele osób − przede wszystkim humanistów − którym
matematyka nie jest potrzebna i mogą mieć problem ze zdaniem z niej matury. Według mnie,
człowiek po liceum powinien mieć wszechstronną wiedzę a przynajmniej znać podstawy takich
przedmiotów jak matematyka. Jakby nie patrzeć poziom obecnej matury podstawowej z matematyki,
jest tak niski, że na jej zdanie wystarcza spokojnie wiedza z gimnazjum. Tak więc można się
zastanowić, czy osoba kończąca 3 klasę liceum i niepotrafiąca jej zdać, faktycznie nadaje się
na to, aby iść na studia?
11 lip 01:41
Basia: Opowiem Wam bajkę.
Wcale nie dawno temu, i nie za siedmioma górami, ani nie za siedmioma lasami, tylko tu i teraz
był sobie mały Jaś.
Jaś, jak każde dziecko, był ciekawy świata, więc jak widział na kartkach zagryzmolonych przez
rodziców jakieś dziwne znaczki pytał co to jest. Odpowiedź na ogół otrzymywał krótką i
wezłowatą, i tą metodą mniej więcej w wieku lat pięciu wiedział, że ten gryzmoł ∫ to całka,
ten ∑ suma nieskończona itd.
I tyle. Nikt się nie palił, żeby mu koniecznie tłumaczyć co to jest, przynajmniej dopóki nie
pytał.
Oczywiście przyszedł taki moment, że pytać zaczął i wtedy tata wyjaśnił mu, że aby zrozumieć
najpierw musi nauczyć się paru innych rzeczy. Dostał kilka książek w rodzaju "I Ty możesz być
Pitagorasem" i na jakiś czas zapanował spokój.
Spokój trwał do momentu, w którym w szkole pojawiły się trójkąty 30−60−90 i trójkąt
równoboczny.
Jaś z przyczyn bliżej nieznanych uparł się, że nie będzie sobie głowy zawracał pamiętaniem
jakichś idiotycznych wzorków, które w trzy sekundy można wyprowadzić z tw.Pitagorasa. I nie
pamiętał, programowo. Rodzice Jasia jakoś to przetrwali, nauczycielka też, chociaż nie bez
zgrzytów.
Podobny kryzys pojawił się przy trygonometrii. Jaś zapamiętania wzorków na tg(α±β), ctg(α±β),
tg(2α) i ctg(2α) odmówił kategorycznie. Ponieważ jednak szybciej je sobie z wzorków na sinus i
cosinus wyprowadzał niż inni pisali z pamięci dano mu święty spokój.
A potem jeszcze przy czymś i jeszcze, i jeszcze. Już naprawdę wszystkiego nie pamiętam.
Poza tym Jaś był całkiem normalnym chłopcem. Miał dziewczyny i dwa tysiące innych
zainteresowań. Nawet w olimpiadzie nie startował. Nie miał ochoty i nie musiał.
Wybrał sobie studia interdyscyplinarne, i ostatecznie został informatykiem.
Jaś jest dzisiaj całkiem dorosłym panem Janem, w lipcu stuknie mu trzydziestka. We wrześniu
otworzy swój przewód habilitacyjny. Doktoryzował się cztery lata temu.
11 lip 09:04
Artur_z_miasta_Neptuna:
Gustlik −−−− humanista też musi logicznie myśleć −−− a więc, trudniejsza matura (czyli większa
ilość dowodów − jak najbardziej).
40% oblanych matur? I bardzo dobrze −−− nie każdy MUSI iść na studia. Nie każdy MUSI mieć
maturę −−− sprawdź jakie procenty (ilość z maturą do ilości uczniów w wieku maturalnym) były
'za Twoich czasów' ... a jakie są obecnie.
To co −−− jak 'za Twoich lat' 'ślisłowiec' oblał maturę z polskiego (co było rzeczą nietrudną)
to co mógł zrobić? Odwoływać się? Pisać poprawkę w sierpniu? Niee .... szedł do woja i za rok
mógł jeszcze raz.
Obecnie trochę zbytnio 'cackamy' się z młodziakami (dziwnie do brzmi, bo niedawno ja też nim
byłem).
I nadal nie odpowiedziałeś mi na pytanie − czy miałeś styczność z jakimkolwiek maturzystą,
który NIE zdał matury z matematyki w ciągu ostatnich 2 lat?
Liczba punktów za dowody w wysokości (powiedzmy) 25−35% nie przekreślają szans na zdanie matury
... a więc nadal czysto rachunkowa część wystarczy na zdanie matury.
Poza tym − z pewnością wycofanie się z części testowej byłoby krokiem w stronę 'jakości'.
Chyba, ze polska matura ma (w przyszłości) nie odbiegać od amerykańskiego egzaminu, który jest
w stanie rozwiązać średnio rozgarnięty 6−klasista na conajmniej 60%.
Przykładowe zadanie z 'amerykańskiej matury'
Punkt A ma współrzędne (1,0), punkt B ma współrzędne (3,6). Środkiem odcinka AB jest:
a) C=(−1,0)
b) C=(2,3)
c) C=2√10
d) C=(4,6)
e) C=(2,6)
(widnieje 'okratkowany' rysunek obok zadania z zaznaczonym odcinkiem i punktami A,B)
Czy to jest zadanie 'na poziomie' przyszłego studenta? Przyszłości naszego narodu? Projektanta
mostów, samolotów czy chociażby pani siedzącej w okienku w banku?
11 lip 09:11
Basia: Poza tym:
Najważniejszymi rzeczami w matematyce są
logika i teoria mnogości.
Wszystko inne jest z tego, chociaż może się to czasami wydawać dziwne.
Kto tego nie wie, matematykiem
nie jest, nie był i nie będzie 
11 lip 09:12
Gustlik: Vax znowu przekręcasz moje słowa. Napisałem [P["dowody matematyczne są najmniej
potrzebne", a nie "matematyka nie jest potrzebna", a to dwie różne rzeczy. Nie twierdzę
wcale, że dowody są niepotrzebne, ale nie mogę zaczaić, jakimi kryteriami kierowało się MEN i
CKE, że łatwe rzeczy, np. wektory wywalili na rozszerzenia, a trudne − dowody i "kręte
ścieżki" zostawili na podstawach. Owszem − masz rację, że powinno się zwiększyć ilość zadań na
dowodzenie w szkołach. I do tego skoro trudne dowody są na podstawach to na podstawy powinny
tez wrócić te łatwe rzeczy, jak np. wektory i o t mi przede wszystkim chodzi.
11 lip 10:48
Gustlik: Co do "amerykańskiej matury" też nie jestem zwolennikiem obniżania poziomu, bo przez to ten
program z matematyki jest taki popaprany, co do tego Arturze masz rację. Uważam, że
należałoby zlikwidować zadania zamknięte i w zamian za to wprowadzić zadania otwarte szybkiej
odpowiedzi (bez odpowiedzi ABCD), zeby uczeń sam dochodził do wyniku, a nie zgadywał albo
próbował podpasować odpowiedź. Testy dobre są ale na historii czy biologii, a nei na
matematyce.
11 lip 10:52
Gustlik: Arturze, jak chcesz wiedzieć, miałem styczność z maturzystami, którzy nie zdali matury,
choć były to nieliczne przypadki. Niemniej były to osoby słabe lub leniwe. Ci, których uczę,
zdają maturę m.in. dlatego, że znaja krótkie metody.
11 lip 10:57
Jasper: Gustliku nie wiem dlaczego tak się upierasz przy wektorach. Szczerze Ci powiem, że na
rozszerzeniu w LO tylko liznęliśmy nieznacznie ten temat. Do porządku nauczyłem się ich
dopiero na studiach. Jest to temat którego nie cierpię w matematyce i musiałem spędzić długie
godziny żeby się w nich zagłębić. Jest tam cała masa wzorów, zależności, rozróżnia się
iloczyny skalarne, wektorowe, jedne liczy się tak inne inaczej. Osobiście uważam, że temat ten
jeśli nie jest komuś "pisany" − jak np. Tobie, to wcale nie jest taki prosty jak piszesz.
Jeśli chodzi o mnie to wystrzegam się ich jak ognia i korzystam tylko w nielicznych
przypadkach kiedy inne metody zawodzą.
11 lip 11:20
Gustlik: Jasper, bo Cię ich nie nauczono. A wektory sa naprawdę łatwe, o wiele łatwiejsze od
"bezwektorowych" metod. Moi uczniowie je rozumieją.
11 lip 11:28
Basia:
P.S.
To nie wzór
rumpka jest z wyznacznika; to użycie wyznacznika pary wektorów wynika z tego
wzoru.
Wyprowadza się to tak:
1. wylicza się analitycznie cosα z tw.cosinusów (i zauważa związek z iloczynem skalarnym)
2. wylicza się analitycznie sinα z 1 trygonometrycznej
| | |xa*yb − ya*xb| | | |xa*yb − ya*xb| | |
dostaje się sinα= |
| = |
| |
| | |a→|*|b→| | | a*b | |
3. w tym momencie dopiero zauważa się, że to jest wartość bezwzględna z wyznacznika macierzy
współrzędnych wektorów, nazywa wyznacznikiem pary wektorów i zaczyna używać
4. podstawia się do wzoru P=
12absinα
co nie zmienia faktu, że jak się to już rozumie, to zadanie rozwiązuje się szybko. Nawet
bardzo.
11 lip 11:33
Leszek: Gustlik, wektory są łatwe do nauczenia ale Twoi uczniowie uczą się ich na pamieć jak komputer
wykonywania zaprogramowanych algorytmów. A prawda jest taka że egzamin z matematyki powinien
być egzaminem z inteligencji a nie z pamięci.
11 lip 11:33
Gustlik: Leszku, a co "nieinteligentnego" widzisz w prostych metodach, np. wektorach czy schemacie
Hornera? Ja im pokazuję, skąd to się wzięło, udowadniam im wzory a potem stosuję.
11 lip 11:43
Gustlik: Basiu i znów wychodzi na moje. Nie lepiej udowodnić ten wzór na pole (zrobi się to tylko
raz), a potem go stosować w zadaniach i ten czas poświecony na udowodnienie wzoru zwróci sie z
nawiązką? A uczen znając sposób piorunem rozwiąże takie zadanie na maturze?
11 lip 11:48
Basia:
szczególnie na forum świetnie Ci to wychodzi; nie mówię o stałej pracy z uczniem
to są dwa różne światy
11 lip 12:17
picia:
najlepsza to jest ta bajka
Basi 
ps najlepsza metoda to taka ktora doprowadza do poprawnego rozwiazania

11 lip 12:26
Leszek: Gustlik:"Ja im pokazuję, skąd to się wzięło, udowadniam im wzory a potem stosuję."Thaa myślisz
że oni to rozumieją? A nawet jeśli rozumieją to padną jak coś się zmieni. Inteligentni to oni
nie są skoro musisz im to pokazywać. A jak będzie co innego(w tym te zadania na dowodzenie) to
jak im pokażesz jak to rozwiązać.Musisz uczyć swoich uczniów myślenia uniwersalnego a nie
tylko w konkretnych przypadkach. A takie objekty jak wektory , macierze i ich wyznaczniki są
abstrakcyjne i dla humanisty będzie to tylko nauka gotowych objektów.Taki humanista nie nauczy
się tworzyć swoich "objektów" by rozwiązywać problemy z wiązane z logiczną inteligencją.
11 lip 12:44
Gustlik: Leszku ja uczę myślenia uniwersalnego, bo uczeń wie wtedy, jaką metodę dobrać do zadania,
zna proste sposoby i dzięki temu zdaje maturę.
11 lip 22:34
Basiek: Witajcie

Wtrącę się, jeśli pozwolicie.

Cała ta dyskusja (wybaczcie) jest w dużym stopniu pozbawiona
sensu (wybaczcie). Wzajemnie próbujecie przekonać się do własnych poglądów, a tak naprawdę to
WSZYSTKO zależy od tego, komu tę wiedzę przekazujecie.

W mniejszym stopniu od Was, od
sposobu, od warunków.
11 lip 22:53
 ?
?
 2
linijki
2
linijki
 P.S. Tak wiem nie jestem Basią
P.S. Tak wiem nie jestem Basią 


 Sam wielokrotnie pisałeś, ze
matura to stres −−− no to co pocznie biedny (słaby) maturzysta który nagle zapomni jak się
liczyło wyznacznik? Panika ... gryzienie pazurów ... załamanie nerwowe ... itd. itp.
A człek mało inteligentny (bo taki nie zdał matury podstawowej) tychże wzorów znać nie będzie
Sam wielokrotnie pisałeś, ze
matura to stres −−− no to co pocznie biedny (słaby) maturzysta który nagle zapomni jak się
liczyło wyznacznik? Panika ... gryzienie pazurów ... załamanie nerwowe ... itd. itp.
A człek mało inteligentny (bo taki nie zdał matury podstawowej) tychże wzorów znać nie będzie
 Pomijając całą resztę wzorów, które byłyby pomocne w 'szybszym' zrobieniu innych zadań.
Gustlik −−− metoda wektorowa jest cudowna pod warunkiem, że się wie (i pamięta) co to jest
iloczyn wektorowy i jak się wylicza wyznacznik macierzy 3x3 −−− a z tym ma problemy minimum
~50% studentów kierunków technicznych bądź finansowych.
Dlatego też nie rozumiem dlaczego chcesz nam na siłę (poniekąd) wmówić, że gdyby 'krótsze'
metody były stosowane przez WSZYSTKICH nauczycieli to zdawalność matury byłaby większa.
Gustlik −−− ile uczni za Twoich czasów zdawało maturę (jaki procent kończących średnią szkołę
podchodziło do matury i ją zdawało)
A ile jest obecnie? Czy procent 'inteligentnych' uczniów się zwiększył? Nie ... więc niby
dlaczego teraz ma dojśc do tego, że 100% uczniów kończących szkołę średnią ma zdać maturę?
A co do pola czworokąta −−− mam nadzieję, ze nie mówisz o polu dowolnego czworokąta, bo jeżeli
tak to wybacz ale śmiem się nie zgodzić.
Pomijając całą resztę wzorów, które byłyby pomocne w 'szybszym' zrobieniu innych zadań.
Gustlik −−− metoda wektorowa jest cudowna pod warunkiem, że się wie (i pamięta) co to jest
iloczyn wektorowy i jak się wylicza wyznacznik macierzy 3x3 −−− a z tym ma problemy minimum
~50% studentów kierunków technicznych bądź finansowych.
Dlatego też nie rozumiem dlaczego chcesz nam na siłę (poniekąd) wmówić, że gdyby 'krótsze'
metody były stosowane przez WSZYSTKICH nauczycieli to zdawalność matury byłaby większa.
Gustlik −−− ile uczni za Twoich czasów zdawało maturę (jaki procent kończących średnią szkołę
podchodziło do matury i ją zdawało)
A ile jest obecnie? Czy procent 'inteligentnych' uczniów się zwiększył? Nie ... więc niby
dlaczego teraz ma dojśc do tego, że 100% uczniów kończących szkołę średnią ma zdać maturę?
A co do pola czworokąta −−− mam nadzieję, ze nie mówisz o polu dowolnego czworokąta, bo jeżeli
tak to wybacz ale śmiem się nie zgodzić.

 no to może jeszcze coś takiego dla chętnych :
| 1 xA yA |
PΔ= 12* | | 1 xB yB | | ,
| 1 xC yC |
no to może jeszcze coś takiego dla chętnych :
| 1 xA yA |
PΔ= 12* | | 1 xB yB | | ,
| 1 xC yC |

 . (mój cichy pretendent to Poznań). No nic do 16 mam czas
. (mój cichy pretendent to Poznań). No nic do 16 mam czas  .
.
 Zastosować metodę trapezów
1. Trapez KACM
Zastosować metodę trapezów
1. Trapez KACM

 W
karcie wzorów również jest, więc nie widzę problemu
W
karcie wzorów również jest, więc nie widzę problemu 

 Właśnie mi przypomniałeś! ( lody w zamrażarce czekają ... "Magnum almond"
Właśnie mi przypomniałeś! ( lody w zamrażarce czekają ... "Magnum almond"  Co ja bym bez Ciebie zrobiła
Co ja bym bez Ciebie zrobiła 








 .
.
 xn | yn | yn + 1 − yn − 1 | xn(yn + 1 − yn − 1)
1 1 −7 −7
2 2 8 16
3 9 −1 −3
2P = −7 + 16 − 3 ⇒ P = 3
xn | yn | yn + 1 − yn − 1 | xn(yn + 1 − yn − 1)
1 1 −7 −7
2 2 8 16
3 9 −1 −3
2P = −7 + 16 − 3 ⇒ P = 3


 Vax, Znam wzór Picka. Ale wtedy trzeba wykonać dokładny rysunek, zliczyć punkty kratowe,
zarówno wewnętrzne jak i te na obwodzie, co przy niewielkiej nawet niedokładności może
generować błędy. Niektóre z tych punktów mogą się znaleźć bardzo blisko któregoś z boków
figury i przy niewielkiej nawet niedokładności mogą zostać uznane przez ucznia za punkty na
obwodzie figury, podczas gdy faktycznie leżą one na zewnątrz albo wewątrz figury i już jest
błąd. Albo punkty leżące na zewnątrz figury mogą się znaleźć wewnątrz niej.
Natomiast metoda wektorowa nie wymaga nawet rysunku lub co najwyżej rysunek poglądowy, jak np.
ten powyżej:
Vax, Znam wzór Picka. Ale wtedy trzeba wykonać dokładny rysunek, zliczyć punkty kratowe,
zarówno wewnętrzne jak i te na obwodzie, co przy niewielkiej nawet niedokładności może
generować błędy. Niektóre z tych punktów mogą się znaleźć bardzo blisko któregoś z boków
figury i przy niewielkiej nawet niedokładności mogą zostać uznane przez ucznia za punkty na
obwodzie figury, podczas gdy faktycznie leżą one na zewnątrz albo wewątrz figury i już jest
błąd. Albo punkty leżące na zewnątrz figury mogą się znaleźć wewnątrz niej.
Natomiast metoda wektorowa nie wymaga nawet rysunku lub co najwyżej rysunek poglądowy, jak np.
ten powyżej:

 ps najlepsza metoda to taka ktora doprowadza do poprawnego rozwiazania
ps najlepsza metoda to taka ktora doprowadza do poprawnego rozwiazania
 Wtrącę się, jeśli pozwolicie.
Wtrącę się, jeśli pozwolicie.  Cała ta dyskusja (wybaczcie) jest w dużym stopniu pozbawiona
sensu (wybaczcie). Wzajemnie próbujecie przekonać się do własnych poglądów, a tak naprawdę to
WSZYSTKO zależy od tego, komu tę wiedzę przekazujecie.
Cała ta dyskusja (wybaczcie) jest w dużym stopniu pozbawiona
sensu (wybaczcie). Wzajemnie próbujecie przekonać się do własnych poglądów, a tak naprawdę to
WSZYSTKO zależy od tego, komu tę wiedzę przekazujecie.  W mniejszym stopniu od Was, od
sposobu, od warunków.
W mniejszym stopniu od Was, od
sposobu, od warunków.