 Proponuję takie rozwiązanie problemu,innego sposobu nie widzę
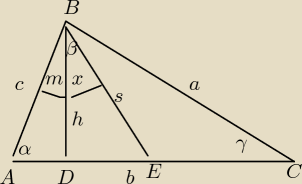
Przyjąłem kąty:
α = 6oo 37' , β = 78o 35' , γ = 40o48'
BD − wysokość , BE − środkowa
Przyjmuję bok a = 8 i dobieram boki b i c tak by tworzyły trójkąt
o podanych kątach
Proponuję takie rozwiązanie problemu,innego sposobu nie widzę
Przyjąłem kąty:
α = 6oo 37' , β = 78o 35' , γ = 40o48'
BD − wysokość , BE − środkowa
Przyjmuję bok a = 8 i dobieram boki b i c tak by tworzyły trójkąt
o podanych kątach
| a*sin(β) | a*sin(γ) | |||
b = | = 9 , c = | = 6 | ||
| sin(α) | sin(α) |
| (b/2) | s | b*sin(α) | |||
= | => sin(n) = | = 0.5519 | |||
| sin(n) | sin(α) | 2*s |

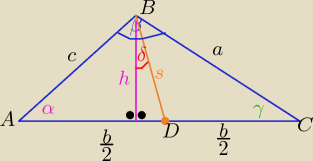
| h | ||
cosδ= | ||
| s |
| 1 | ||
długość środkowej s= | √2a2+2c2−b2 ( stosuję gotowy wzór) | |
| 2 |
| a | b | c | ||||
z tw. sinusów dla ΔABC : | = | = | ||||
| sinα | sinβ | sinγ |
| b*sinγ | b*sinα | |||
wynika że : c= | i a= | |||
| sinβ | sinβ |
| b*h | c*a | |||
Ze wzoru na pole ΔABC : | = | *sinβ | ||
| 2 | 2 |
| b*sinγ*sinα | ||
mamy: h= | ||
| sinβ |
| b | ||
s= | √2sin2α+2sin2γ−sin2β | |
| 2sinβ |
| h | 2sinγ*siα | |||
zatem: cosδ= | = | |||
| s | √2sin2α+2sin2γ−sin2β |
 dla AS
dla AS 
 brawo dla Ety.
brawo dla Ety.
 "jutro" podam swój sposób i wychodzi mi kąt ≈ 16o.
"jutro" podam swój sposób i wychodzi mi kąt ≈ 16o.
| AE | BE | CE | BE | ||||
= | i | = | ⇔ | ||||
| sin(m) | sinα | sin(n) | sinγ |
| AE | s | AE | s | |||||
⇔ | = | i | = | ⇔ | ||||
| sin(90o−α+x) | sinα | sin(90o−γ−x) | sinγ |
| AE | s | AE | s | |||||
⇔ | = | i | = | i dzieląc stronami ⇒ | ||||
| cos(α−x) | sinα | cos(γ+x) | sinγ |
| cos(α−x) | sinα | |||
⇒ | = | ⇔ | ||
| cos(γ+x) | sinγ |
| cosαcosx+sinαsinx | sinα | |||
⇔ | = | ⇔ | ||
| cosγcosx−sinγsinx | sinγ |
| cosx (cosα+sinα tgx) | sinα | |||
⇔ | = | ⇔ | ||
| cosx (cosγ−sinγ tgx) | sinγ |
| cosα+sinα tgx | sinα | |||
⇔ | = | ⇔ | ||
| cosγ−sinγ tgx | sinγ |
| sin(α−γ) | ||
⇔ tgx = | . ....  | |
| 2sinαsinγ |
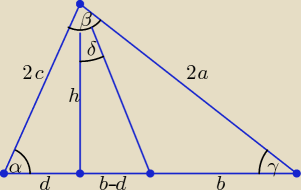 Proponuję takie rozwiązanie:
sinβ = sin[180o − (α + γ)] = sin(α + γ) = sinα*cosγ + sinγ*cosα
Proponuję takie rozwiązanie:
sinβ = sin[180o − (α + γ)] = sin(α + γ) = sinα*cosγ + sinγ*cosα
| h*cosα | ||
d = h*ctgα = | , | |
| sinα |
| h | h | |||
2c = | , 2a = | |||
| sinα | sinγ |
| 1 | 1 | |||
Pole trójkąta P = | *2b*h = bh i P = | *2c*2a*sinβ | ||
| 2 | 2 |
| 1 | h | h | hsinβ | |||||
Stąd: bh = | * | * | *sinβ ⇒ b = | |||||
| 2 | sinα | sinγ | 2sinαsinγ |
| hsinβ | h*cosα | h(sinβ − 2sinγcosα) | ||||
b − d = | − | = | = | |||
| 2sinαsinγ | sinα | 2sinαsinγ |
| h(sinαcosγ + sinγcosα − 2sinγcosα) | hsin(α − γ) | |||
= | = | |||
| 2sinαcosγ | 2sinαsinγ |
| b − d | sin(α − γ) | |||
tgδ = | = | |||
| h | 2sinαsinγ |
 no i jak widać warto myśleć i jedno zadanie "robić" na kilka sposobów , aby zdobyć
doświadczenie przez wyciąganie wniosków, co warto, a co nie i nie zatrzymywać się na jednym
wyuczonym schemacie , bo że to niby dzięki niemu "wszyscy" zdadzą , a dlaczego
no i jak widać warto myśleć i jedno zadanie "robić" na kilka sposobów , aby zdobyć
doświadczenie przez wyciąganie wniosków, co warto, a co nie i nie zatrzymywać się na jednym
wyuczonym schemacie , bo że to niby dzięki niemu "wszyscy" zdadzą , a dlaczego  , przecież
nie muszą wszyscy zdać
, przecież
nie muszą wszyscy zdać  i tyle .
i tyle .
