nie wiem jak to zrobić anka: Wpłacamy 300 zł.co pół roku przez cztery lata (pierwszego stycznia i pierwszego lipca) na konto oprocentowane 10 % w skali roku z półroczną kapitalizacją odsetek. Jaką sumą będziemy dysponowali po 4 latach?

pazio:

	5%		21
kn = 300*(1+		)8 = 300*(		)8
	100%		20

ale to to już sama sobie policz

imię lub nick: jeśli dobrze zrozumiałem treść zadania, to rozwiązanie powinno wyglądać tak: (300+0,05*300) + 300 −po pierwszej kapitalizacji [(300+0,05*300) + 300] + 0,05[(300+0,05*300) + 300] + 300 −po drugiej kapitalizacji {[(300+0,05*300) + 300] + 0,05[(300+0,05*300) + 300] + 300} + 300 −po trzeciej kapitalizacji ({[(300+0,05*300) + 300] + 0,05[(300+0,05*300) + 300] + 300} + 300) + 0,05({[(300+0,05*300) + 300] + 0,05[(300+0,05*300) + 300] + 300} + 300) + 300 − po czwartej kapitalizacji ... aż do ośmiu kapitalizacji. Na kalkulatorze to łatwo policzyć, ale może da się wyprowadzić jakiś ogólny wzór na ten ciąg. Gdyby sprawdził to Bogdan lub ktokolwiek i mnie uświadomił byłbym wdzięczny.

imię lub nick: aha.. wyszło mi 3007,97

imię lub nick: nikt się nie wypowie na ten temat? ... mam jeszcze raz to zadanie dodać?

Tomek: imię lub nick: słuchaj, k=300, p=10% półroczna kapitalizacja odsetek czyli w ciągu roku masz dwa okresy rozliczeniowe. Przez cztery lata daje ci osiem takich okresów n=8, p:2=5% Przez ten cały czas nic z kasą nie robisz i wypłacasz dopiero na koniec. Popatrz: 100%+5%=105%=1,05 (1,05*300) − stan konta po jednym okresie 1,05*(1,05*300) = 1,05²*300 − stan konta po dwóch okresach 1,05*1,05²*300=1,05³*300 − stan po trzech okresach itd. tworzy się wzór rekurencyjny: (100+p)%ⁿ*k 1,05ⁿ*300=1,05⁸*300

imię lub nick: W treści zadania jest napisane: "Wpłacamy 300 zł.co pół roku przez cztery lata..." zrozumiałem to tak że po każdej kapitalizacji odsetek dokładamy trzy stówki i procent jest już liczony od kwoty zwiększonej o te trzy stówki wraz z wcześniej doliczonym procentem. Najwyraźniej nie mam racji. dzięki za wyjaśnienie.

Bogdan: imię lub nick − nie rezygnuj ze swojego rozumowania. Dzisiaj jestem zajęty, ale jeśli nikt nie zajmie się tym problemem, to spróbuję w wolnym czasie wyprowadzić wzór ogólny dla podobnych sytuacji przyjmując oznaczenia: p% − roczna stopa procentowa, m − liczba określająca ile razy w roku następuje kapitalizacja, n − liczba lat, K − stała kwota wpłacana na początku każdego okresu, K_K − kwota końcowa.

Tomek: imię lub nick − masz rację z tymi wpłatami co pół roku popróbuję coś zrobić z oznaczeniami jak u Bogdana

imię lub nick: jak narazie doszedłem do tego że K można zapisać poza nawiasem i ich ilość będzie równa m. Jednak sprawa komplikuje się z kwotom od której jest liczony procent. Zastanawiam się czy to nie wykracza poza moje umiejętności.

imię lub nick: ^{(dysortografia dała o sobie znać)}

Squall: Można spróbować zapisać po pierwszej kapitalizacji: 300+300*0,05 a przy każdej następnej kapitalizacji zapisywać 300+x*0,05 gdzie x oznacza wynik po poprzedniej kapitalizacji Tylko wynik strasznie duży mi wychodzi

Squall: Eh...błąd mi się wkradł w obliczenia. imię lub nick − wynik wyszedł mi dokładnie taki sam jak Tobie

Tomek: Już wiem i wychodzi dobrze: E − wkład równy Wpłaty są z góry r=0,05 q=1+0,05=1,05 n=8 E=300 K E₁ E₂ E₃ −−−−−|−−−−−−−−−−−|−−−−−−−−−−−|−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−− 0 1 2 K₁=E₁q+E₂ K₂=K₁q+E₃=E₁q²+E₃ ...... K_n=E₁qⁿ+E₂qⁿ⁻¹+...+E_n+1 dla wkładów równych E_j=E

	qn−1
Kn=Eq
	q−1

	1,058−1
Kn=300*1,05*
	1,05−1

K_n=3007,97 Chyba będzie zrozumiałe

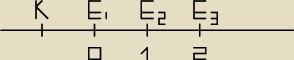
Tomek: trochę rysunek mi nie wyszedł ten będzie bardziej widoczny

Tomek: dosyć na dziś trochę to zadanie mi zajęło ale nie mogłem mu podarować

Bogdan: Ja też nie mogłem mu podarować. Oznaczenia takie, jak podałem wyżej.

	100m		p
KK = K * (1 +		) * [ (1 +		)mn − 1]
	p		100m

Proszę o zweryfikowanie tego wzoru.

Bogdan: W tym zadaniu: K = 300 m = 2 p = 10 n = 4

Tomek: widzę Bogdan, że też jesteś zapaleńcem

imię lub nick: gratuluję rozwiązania Tomku. w sumie dalej nie potrafię wyprowadzić tego wzoru, ale na maturze tego raczej nie będzie.