Logika Szaj-bus: Prawdziwe jest zdanie: Nieprawda, że jeśli Platon założył Akademie, to jeśli Arystoteles był uczniem Platona, to Arystoteles nie uczęszczał do Akademii. Czy na podstawie tej informacji można udzielić odpowiedzi na poniższe pytania (jeśli tak, to daj te odpowiedzi). a) Czy Platon założył Akademię? b) Czy Arystoteles był uczniem Platona? c) Czy Arystoteles uczęszczał do Akademii? Mógłby ktoś rozwiązać to zadanie i wytłumaczyć krok po kroku jak to zrobić. Z góry dziękuję.

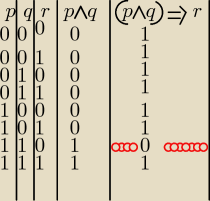
Artur z miasta Neptuna: gdzie: p −−− Platon założył Akademie q −−− Arystoteles był uczniem Platona r −−− Arystoteles nie uczęszczał do Akademii z tabelki wynika, że ów zdanie, skoro jest prawdziwe (czyli wynikiem przed zaprzeczeniem jest 0 ) tylko dla sytuacji p=1, q=1 i r=0 czyli gdy: Platon założył Akademie Arystoteles był uczniem Platona oraz Arystoteles uczęszczał do Akademii

Jack: zadanka z książki p. Stanosz?

Sławek: p: Platon założył Akademię q: Arystoteles był uczniem Platona r: Arystoteles uczęszczał do Akademii Nieprawda, że jeśli Platon założył Akademię, to jeśli Arystoteles był uczniem Platona, to Arystoteles nie uczęszczał do Akademii. ~[p ⇒ (q ⇒ ~ r)] ⇔ p ⋀ ~( q ⇒ ~ r) ⇔ p ⋀ q ⋀ ~(~ r) ⇔ p ⋀ q ⋀ r

Szaj-bus: Sławek a uzasadnisz te przeinaczenia

Basia: Sławka już nie ma więc Ci odpowiem. Sławek korzysta tutaj tylko z jednego prawa rachunku zdań; mianowicie z tego ~[p⇒q] ⇔ p∧~q a to prawo bardzo łatwo udowodnić metodą 0−1 (w logice uważa się to prawo za powszechnie znane i już bez dowodu wykorzystuje w takich zadaniach jak to, ale przekonać się, że rzeczywiście jest tautologią zawsze warto; szybciej się je wtedy zapamięta)

Basia: no i z tego, że ~(~r) ⇔ r ale to już chyba nie wymaga komentarza

Cris: dzieki za wytłumaczenie, też tego potrzebowałem

Marry: Może ktoś jeszcze raz napisać jak zrobić to zadanie bo wogóle go nie rozumiem. Z góry dzięki