Prosze o pomoc rex: wykaż że jeśli:

x		y		z		a		b		c
	+		+		= 1 i		+		+		= 0 ,
a		b		c		x		y		z

	x2		y2		z2
to		+		+		= 1
	a2		b2		c2

gdzie a,b,c,x,y,z są różne od zera No tego zadania to już wogóle niewiem jak nawet zacząć , ono jest jakieś z kosmosu bardzo prosze o rozwiązanie tego i wytłumaczenie

Vax:

x

y

z

x

x2

xy

xz

x

+

+

= 1 /*

<=>

+

+

=

a

b

c

a

a2

ab

ac

a

	x2		x		xy		xz
<=>		=		−		−
	a2		a		ab		ac

Analogicznie:

y2		y		xy		yz
	=		−		−
b2		b		ab		bc

z2		z		xz		yz
	=		−		−
c2		c		ac		bc

Więc:

x2		y2		z2		x		y		z
	+		+		=		+		+		−
a2		b2		c2		a		b		c

xy

xz

yz

xy

xz

yz

2(

+

+

) = 1 − 2(

+

+

)

ab

ac

bc

ab

ac

bc

a

b

c

xyz

xy

xz

yz

Ale

+

+

= 0 /*

<=>

+

+

= 0

x

y

z

abc

ab

ac

bc

	x2		y2		z2
Czyli istotnie		+		+		= 1 cnd.
	a2		b2		c2

Eta:

a		1		b		1		c		1
	=		,		=		,		=
x		x   a		y		y   b		z		z   c

to:

a

b

c

1

1

1

x

y

z

+

+

=

+

+

=0 /*

*

*

x

y

z

x   a

y   b

z   c

a

b

c

y

z

x

z

x

y

to:

*

+

*

+

*

=0

b

c

a

c

a

b

	x		y		z
Teraz równość		+		+		= 1 /2
	a		b		c

x2

y2

z2

x

y

x

z

y

z

+

+

+2*(

*

+

*

+

*

)=1

a2

b2

c2

a

b

a

c

b

c

	x2		y2		z2
		+		+		+ 2*0= 1
	a2		b2		c2

	x2		y2		z2
		+		+		=1
	a2		b2		c2

c.n.u

Eta:

rex: ok wielkie dzięki za rozwiązanie

pigor: ... no, to ja ... wyciągając wnioski z waszych rozwiązań, za które bardzo dziękuję, widzę to tak : z założenia

x

y

z

a

b

z

xyz

+

+

=1 / 2 i

+

+

=0 / *

⇒

a

a

c

x

y

c

abc

x2

y2

z2

xy

yz

xz

⇒

+

+

+2(

+

+

)=1 i

a2

b2

c2

ab

bc

ac

xy

yz

xz

x2

y2

z2

i

+

+

=0 ⇒

+

+

=1 c.n.w. . ...

ab

bc

ac

a2

b2

c2

pigor:

	a		b		c		xyz
... oczywiście tam powinno być ... i		+		+		=0 / *		, przepraszam
	x		y		z		abc

Eta:

Eta: Witam Widzę,że nie macie co robić w taki upał zad1/ Wykaż,że jeżeli suma długości wysokości trójkąta jest 9 razy większa od długości promienia okręgu wpisanego w ten trójkąt, to trójkąt jest równoboczny. zad2/ Wykaż, jeżeli punkty D, E,F są rzutami prostokątnymi punktu P leżącego wewnątrz trójkąta równobocznego ABC odpowiednio na boki BC, AC, AB , to zachodzi równość:

	|PD|+|PE|+|PF|		√3
		=
	|BD|+|CE|+|AF|		3

Eta:

Basia: Upał, Eto, upał.................

Eta: Oj tak, tak ... u mnie 35,3 ..... Uffff jak gorąco, puff jak gorąco ...

Eta: A na forum widzę samych matematycznych pasjonatów Wszystkich pozdrawiam

Basia: U mnie zbiera się na burzę od mniej więcej godziny i zebrać się nie może. A dla mnie ten czas gdy ciśnienie tak strasznie leci w dół jest najgorszy. Zasypiam na stojąco i zaczyna mi się w głowie kręcić. Więc też za chwilę znikam, bo tylko głupoty mogę powypisywać

Vax:

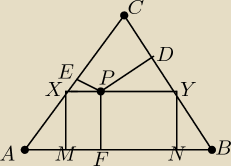
	2P		2P		2P		2P
1) ha+hb+hc = 9r <=>		+		+		= 9 *		/:2P <=>
	a		b		c		a+b+c

1

1

1

9

a+b+c

3

<=>

+

+

=

<=>

=

a

b

c

a+b+c

3

1   1   1   + + a   b   c

A tutaj z nierówności między średnią arytmetyczną a harmoniczną otrzymujemy, że równość zajdzie jedynie dla a=b=c cnd. 2) Na początku udowodnię, że |BD|+|CE|+|AF| = |CD|+|AE|+|BF|. Wykażę, że wystarczy rozpatrzeć przypadek, gdy P leży na boku AB. Istotnie, poprowadźmy prostą równoległą do AB przechodzącą przez P i niech tnie ona BC i AC odpowiednio w X,Y. Dodatkowo niech M,N będą rzutami odpowiednio X,Y na AB. Wtedy oczywiście |AM| = |BN| oraz |BY| = |AX|, więc: |YD| + |CE| + |XP| = |CD| + |XE| + |YP| /+|AM|+|AX| <=> (|YD|+|BY|) + |CE| + (|XP|+|AM|) = |CD| + (|XE|+|AX|)+(|YP|+|BN|) <=> |BD| + |CE| + |AF| = |CD| + |AE| + |BF| czyli istotnie wystarczy rozpatrzeć przypadek, gdy P leży na którymś z boków trójkąta. Zauważmy jednak, że zakładając już, że P leży na którymś z boków trójkąta i stosując udowodniony fakt ponownie dostajemy, że wystarczy rozpatrzeć przypadek, gdy punkt P pokrywa się z którymś wierzchołkiem trójkąta ABC, a w takim wypadku teza jest oczywista.

	L		3a
Tak więc pokazaliśmy, że |BD|+|CE|+|AF| =		=		, gdzie a to bok trójkąta. Pokażę
	2		2

	a√3
teraz, że |PD|+|PE|+|PF| =		, istotnie ([XYZ] − pole trójkąta XYZ):
	2

	|BC|*|PD|		2[BPC]		2[BPC]
[BPC] =		<=> |PD| =		=
	2		|BC|		a

Analogicznie:

	2[ACP]		2[APB]
|PE| =		oraz |PF| =
	a		a

	2([APB]+[BPC]+[CPA])		2[ABC]		a2√3   2 *   4
Więc |PD|+|PE|+|PF| =		=		=		=
	a		a		a

	a√3
	2

Tak więc ostatecznie:

|PD|+|PE|+|PF|		a√3   2		√3
	=		=		cnd.
|BD|+|CE|+|AF|		3a   2		3

Eta: dla Vax zad1/ Jeżeli trójkąt jest równoboczny to:

	h
r=		⇒ h=3r
	3

zatem : h+h+h=3r+3r+3r= 9r

pigor: ...lub ad.1) jeśli ktoś nie zauważy równości średnich harm. i arytm., to może dalej ... ¹_a+¹_b+¹_c = ⁹_a+b+c / * (a+b+c) ⇔ ⇔ ^a+b+c_a + ^a+b+c_b + ^a+b+c_c = 9 ⇔ ⇔ 1+^b_a+^c_a + ^a_b+1+^c_b + ^a_c+^b_c+1 = 9 ⇔ ⇔ (*) (^b_a+^a_b) + (^a_c+^c_a) + (^b_c+^c_b) = 6 , a ponieważ równości w nawiasach zachodzą (dowód znany i prosty) odpowiednio ⇔ ⇔ a=b, a=c, b=c, więc (*) zachodzi ⇔ a=b=c (Δ równoboczny) c.n.w. .

pigor: ... i jeszcze raz ja, bo obudziłem się ... z nowym pomysłem na zadanie rex−a w którym chcę pokazać jak niedoceniane wyłączanie przed nawias, robi w tym rozwiązaniu wielką robotę, mianowicie : ^x_a+^y_b+^z_c=1 i ^a_x+^b_y+^c_z=0 ⇒ (^x_a+^y_b+^z_c)²= 1 ⇔

x2

y2

z2

xy

yz

xz

⇔

+

+

+2 (

+

+

) = 1 ⇔

a2

b2

c2

ab

bc

ac

	x2		y2		z2
⇔		+		+		+2*xyzabc (cz+ax+by) =1 . ...
	a2		b2		c2

Eta: Wykaż, że dla a,b,c>0 zachodzi równość:

	a4+b4+c4
		≥abc
	a+b+c

Vax: <=> a⁴+b⁴+c⁴ ≥ a²bc+ab²c+abc²

	2a4+b4+c4
Ale z am−gm mamy:		≥ 4√a8b4c4 = a2bc
	4

	a4+2b4+c4		a4+b4+2c4
Podobnie		≥ ab2c oraz		≥ abc2
	4		4

Po dodaniu stronami otrzymujemy tezę.

Eta:

	a4+b4+c4		a+b+c
Z am−gm :		≥ abc3√abc i		≥3√abc
	3		3

	a4+b4+c4		a+b+c		3
to		≥abc*		/*
	3		3		a+b+c

	a4+b4+c4
		≥abc
	a+b+c

c.n.u

Vax: Hmm wydaje mi się, że w jednym miejscu jest coś nie tak, a konkretnie z tych dwóch nierówności

	a4+b4+c4		a+b+c
nie wynika, że		≥ abc*
	3		3

Eta: Hmm.... no właśnie się zastanawiam

Eta: No to tak : Wiadomo,że prawdziwa jest nierówność x²+y²+z²≥ xy+yz+xz analogicznie a⁴+b⁴+c⁴ ≥ a²b²+b²c² + a²c² =abc(a+b+c)

	a4+b4+c4
		≥abc
	a+b+c

c.n.u.

Eta: Poprawka , nie dopisałam tego przejścia a²b²+b²c²+a²c² ≥ ab*bc+ ab*ac+bc*ac=abc(a+b+c)

pigor: ... to może ja dołożę coś takiego : Wykaż, że jeśli a,b,c>0, to

	1		1		1		a8+b8+c8
zachodzi nierówność :		+		+		≤		.
	a		b		c		a3b3c3

Vax: <=> a⁸+b⁸+c⁸ ≥ a³b³c² + a³b²c³ + a²b³c³

	3a8+3b8+2c8
Ale z am−gm		≥ 8√a24b24c16 = a3b3c2
	8

	3a8+2b8+3c8		2a8+3b8+3c8
Podobnie		≥ a3b2c3 oraz		≥ a2b3c3
	8		8

Po dodaniu stronami otrzymujemy tezę.

pigor: ... lub − analogicznie jak Eta − z oczywistej (chyba już wszyscy co ... chcą ją znają) nierówności np. tak : a⁸+b⁸+c⁸=(a⁴)²+(b⁴)²+(c⁴)² ≥ a⁴b⁴+b⁴c⁴+a⁴c⁴ = = (a²b²)2+(b²c²)²+(a²c²)² ≥ a²b⁴c²+b²c⁴a²+a⁴b²c² = = (ab²c)²+(bc²a)²+(a²bc)² ≥ a²b³c³+b²c³a³+a³b³c² =

1

1

1

1

1

1

= a3b3c3(

+

+

) ⇒ a8+b8+c8 ≥ a3b3c3(

+

+

) ⇒

a

b

c

a

b

c

	1		1		1		a8+b8+c8
⇒		+		+		≤		. c.n.w. . ...
	a		b		c		a3b3c3