pochodna prosze o sprawdzenie hugo: Oblicz pole figury ograniczonej łukiem paraboli y=2x²−x oraz prosta y=x 2x²−x=x x(x−1)= 0 x=0 x=1

	2x3
całka 2x2−x−x dx =		− x2
	3

2 * 13		1
	− 12 = −
3		3

gdzieś jest chyba błąd

Basia: w drugiej linijce x(2x−1) = 0

hugo: 2x² − x − x = 0 czyli 2x² − 2x =0 x² − x =0 ? Basia a wzór całki na pole powierzchni jest poprawny ?

Andrzej: Basiu, nie nie, nie o to chodzi. są dwa błędy Hugo, narysuj sobie jak to wygląda. Po pierwsze, prosta y = x leży "powyżej" tej paraboli, więc zła kolejność w odejmowaniu. Po drugie − całkę z tej paraboli musisz rozbić na przedziały, bo część leży pod osią OX.

hugo: dalej nie rozumiem

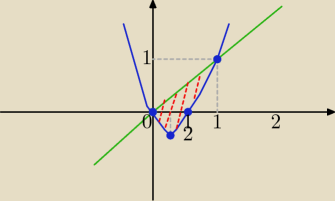
Eta: Teraz tak jak radzi Andrzej dokończ .........

Mila: Według rysunku Ety J=∫₀¹(x−2x²+x)dx= =∫₀¹ (2x−2x²) dx

	1
oblicz, wynik
	3