? Patryk: http://www.zadania.info/d67/1524461 dlaczego tam jest Y_w=b/a+2 nie rozumiem dlaczego b/a w miejsce tego xa

Artur z miasta Neptuna: Poniewaz x jest wspolrzedna wierzcholka − patrz wzor na wspolrzedne wierzcholka paraboli. Taka prosba − mozesz swoje pytania zadawac w jednym temacie i po prostu dopisywac nowe pytania, zamiast tworzyc co rusz nowe watki?

pigor: ,,,, bo z danego równania prostej y=−2x+2 podstawiając (x_w,y_w) ⇒ ⇒ y_w=−2x_w+2 ⇒ −^Δ_4a=−2*(−^b_2a)+2 ⇔ −^Δ_4a=^b_a+2 . ...

Patryk: teraz to wiem dlaczego ,dzięki mogę Artur

Patryk: http://www.zadania.info/d67/6227305 znak wyrażenia E ujemny ?

Eta: No... skoro trójmian ma dwa miejsca zerowe to: Δ>0 ⇒ b²−4ac >0 /*(−1) ⇒ 4ac−b² < 0 zatem E / 4ac−b² ma znak ujemny

Patryk: ok

Patryk: http://www.zadania.info/d67/1844851 skąd w podpunkcie A bierze sie 1/4 2/4 3/4 4/4 ?

Patryk: dobra już wiem

Patryk: http://www.zadania.info/d25/385624 mogło by byc tak ?

⎧	W(2)=W(3)
⎩	W(−1)=W(3)

Eta: Można

Patryk: dzieki AnEta

Patryk: Wyznacz resztę z dzielenia wielomianu w przez: a)(x−3)(x+2), jeżeli reszta z dzielenia wielomianu w przez x−3 wynosi 7 a przez x+2 wynosi −2 kiedyś to umiałem pomożecie ?

Patryk: zamiast −2 jest −3 na koncu

Eta: W(x)= P(x)*(x−3)(x+2) + R(x) , reszta R(x) jest wielomianem stopnia co najwyżej pierwszego zatem R(x)= ax+b z treści zadania W(3)=7 , W(−2)= −3 W(3)= P(3)*(3−3)*(3+2) + 3*a+b ⇒ 3a+b=7 i W(−2)= Q(−2)*(−2+3)*(−2+2) + a*(−2)+b ⇒ −2a+b= −3 Rozwiąż układ równań : 3a+b =7 −2a+b = −3 i podaj resztę R(x)= ax+b =.....

Patryk:

⎧	3a+b=7
⎩	−2a+b=−3	/*(−1)

⎧	3a+b=7
⎩	2a−b=3

5a=10 a=2 b=1 R(x)=2x+1 dzieki

Patryk: a to P(x)=Q(x) jesli chodzi o matematyczny zapis ?

Patryk: http://www.zadania.info/d25/765655 dlaczego akurat miejsca zerowe x²−1 ?

Eta: Masz znaleźć resztę z dzielenia W(x) przez V(x) = x²−1= (x−1)(x+1) zatem pierwiastkami V(x) są x= 1 v x= −1

Patryk: dzieki

Patryk: Zauważyłem błysk pioruna , jego dzwięk usłyszałem 2 sekundy po błysku , czyli znaczy to ,że piorun uderzył w odległości 2920 metrów od mnie ?

Artur z miasta Neptuna: Patryk −−− jaka jest prędkość światła? a jaka prędkość dźwięku ? d −−− odległość v_s − prędkość światła v_d − prędkość dzwięku t − czas dotarcia światła (w sekundach) v_s * t = v_d * (t+2) = d podstaw i wylicz t ... a następnie d

Patryk: chciałem to bardziej intuicyjne zrozumieć ,V_d=1460m/s w ciągu dwóch sekund przebył 2920 m ,czy to się zgadza ?

Artur_z_miasta_Neptuna: i tak i nie tak −−− bo prędkość światła jest o wiele wiele wiele większa niż prędkość dźwięku ... więc t będzie baaardzo małe (ułamek sekundy) nie −−− bo mimo wszystko będzie ten ułamek sekundy, taki potrzebowało światło na przedostanie się od miejsca uderzenia do miejsca obserwacji czyli nie będzie to dokładnie 2920m tylko odrobinę więcej po uwzględnieniu tego wychodzi: 2920,0142 m z tego też względu −−− wystarczy że zrobileś tak jak zrobiłeś (wydawało mi się, że prędkość dźwięku jest większa)

Patryk: już rozumiem to t we wzorze,dzięki

?: Gdyby jakąś maszyna mała sprawność równą 1 to znaczyło by to , ze energie którą pobiera w całości przetwarza ,bez strat ?

Patryk:

Artur_z_miasta_Neptuna: tak

Patryk: mam x√2+2√3<2x teraz powinienem zmienić znak nierówności czy nie ? x√2−2x (?<?) −2√3

Patryk: znaczy powinienem jak podziele wszystko przez √2−2 ? bo √2−2 <0

pigor: .... nie rozumiem cię , więc popatrz jak ja bym do tego podszedł, ale oczywiście możesz po swojemu , a więc może tak : x√2+2√3<2x ⇔ 2√3<x(2−√2) /*(2+√2)>0 ⇔ 2√3(2+√2)<x(4−2) ⇔ ⇔ 2√3(2+√2)<2x /:2 ⇔ √3(2+√2)<x ⇔ x > √3(2+√2 . ...

Patryk: już zrozumiałem mój błąd ale jest taka zasada jesli mnozymy lub dzielimy nierwónosc przez liczbe ujemna to musimy zmienic zwrot nierwonosci ?

Basia: oczywiście: 1 < 2 ale −1 > −2

Patryk: dzięki

Leszek: Patryk Ty wtedy dobrze myślałeś jak podzielisz nierówność x√2−2x < −2√3 przez √2−2 to zmieniasz znak nierówności bo √2−2 <0 więc żadnego błędu nie było

Patryk: dopiero później to zrozumiałem

Patryk: dane sa zbiory A={1,3} B={3,5} czy dopełnienie zbioru A to 5 ?

Patryk: wykaz ,ze równica kwadratów dwóch kolejnych liczb nieparzystych jest liczba podzielna przez 8 można tak ? a=3 b=5 9−25=16 16 dzielni się na 8 ?

pigor: hmm ... , dopełnienie zbioru A (do czego ) jeśli do sumy zbiorów AUB=(1,3,5} , to jest nie 5 tylko zbiór {5} , natomiast dopełnienie do zbioru liczb R, czyli A'= R \ {1,3} , −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a jeśli 2n−1, 2n+1 , gdzie n=1,2,3,... − dwie kolejne liczby nieparzyste , to np. (2n+1)²−(2n+1)²= (2n+1−2n−1)(2n+1+2n−1)= 2*4n= 8n c.n.w. . ...

Eta: Niestety, ale tak nie można 2n−1 , 2n+1 −−− dwie kolejne liczby nieparzyste , n€ N Mamy wykazać,że (2n−1)² − (2n+1)²= 8*k , dla k€C ze wzoru a²−b²=(a−b)(a+b) dla a= 2n−1 i b= 2n+1 zatem L= (2n−1+2n+1)(2n−1−2n−1)= 4n*(−2) = −8n = 8*k . k€ C co kończy dowód

Eta: Wrrr

pigor: ... kurcze mały lapsus, miało być tak : (2n+1)²−(2n−1)²= (2n+1−2n+1)(2n+1+2n−1)= 2*4n= 8n ...

Eta: pigor troszkę pokręciłeś

Eta:

Patryk: dzięki chyba rozumiem

Patryk: wyznacz wszystkie liczby rzeczywiste m takie,że 5m−2 ∊ (−∞;2> jak ?

Basia: 5m−2∊ (−∞;2> ⇔ 5m−2 ≤ 2 rozwiązać i koniec

Patryk: dzieki .

Patryk: dane sa zbiory A=(1:5) B=<4;7> wyznacz zbiór (A∪B)' nie wiem do czego ma być do dopełnienie ?

Patryk: do sumy ,co nie ?

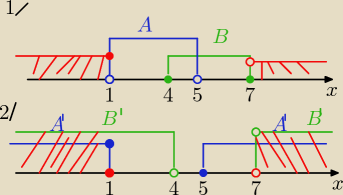
Eta: 1/ AUB= (1, 7> to (AUB)^' = (−∞, 1> U ( 7,∞) lub 2/ To pierwsze prawo de Morgana dla zbiorów (AUB)^'⇔ A^' ∩ B^' to: (AUB)^'= A^'∩ B^'= ( −∞ 1> U (7,∞)

pigor: no, nie masz ten cholerny internet, wikipedię i inne bzdety, zamiast kupić sobie podręcznik do I−szej klasy szkoły średniej − dobry jak ma skorowidz np. polsko−angielski − jak np. "Matematyka się liczy" ; znajdź w skorowidzu hasło "dopełnienie zbioru" i poczytaj na ten temat (przede wszystkim definicję), bo twierdzę, że internet nie nauczy cię matematyki i tyle , a co do zadania : AUB=(1;7> ⇒ (AUB)'=(−∞;1>U(7;+∞) , czyli (AUB)'=R\(AUB)'= R\(1;7> . ...

Basia: [P@pigor]] bez nerwów, tylko spokój może nas uratować ! A czy "pigor" to pitagoras ?

patryk:

patryk: witam mam pytanie ile to jest od 740 odjac 3/5

patryk: zna ktos odpowiedz

qwerk: 739 i 2/5

Patryk: patryk ← to nie ja dzieki

Patryk: jak zamienić 2100 m/min na km/h ?

Patryk: dobra juz mam i wiem

Patryk:

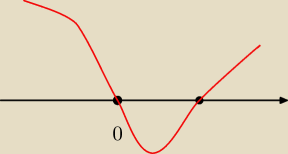
	x3+1
udowodnij ,ze funkcja f(x)=		jest rosnoca w przedziale (−∞;0)
	x2

	x4−2x
[f(x)]'=
	x4

x4−2x
	=0
x4

x⁴−2x=0 x=0 x=³√2 jak widzimy pochodna przyjmuje wartości większe od 0 dla danego przedziału jest ok ?

Patryk: ?

Artur_z_miasta_Neptuna: mały szczególik −−− na szkicu '0' ma być puste (wyjęte z dziedziny − patrz dziedzina funkcji) poza tym −−− dobrze

Patryk: Jak znaleźć sumę kwadratów pierwiastków rowniania kwadratowego zez obliczania jego pierwiastków ? wiem ,ze x₁²+x₂² ale nie umiem tego przekształcić aby zastosować wzory vieta

Patryk: dobra już wiem

Patryk: Wyznacz te wartości parametru m, dla których równanie x²+mx+9=0 ma dwa rozwiązania mniejsze od −1 wiem na pewno Δ>0 ale nie rozumiem ,,dwa rozwiązania mniejsze od −1'' podpowiecie coś ?

pigor: ... , 2 rozwiązania mniejsze od 1 tzn, parabola przecina oś 0X po lewej stronie punktu x=1 na tej osi , a więc niech f(x)=x²+mx+9 i f(x)=0 , to warunki zadania spełnia (opisuje) układ (koniunkcja) nierówności : Δ>0 i x_w<1 i f(1)>0 ⇔ m²−4*9>0 i −^m₂<1 i 1+m+9>0 ⇔ ⇔ |m|>6 i −m<2 i m+10>0 ⇔ (m<−6 lub m>6) i m>2 i m>−10 ⇔ ⇔ −10<m<−6 lub m>6 ⇔ m∊(−10;−6)U(6;+∞) . ...

Mila: Pigor od (−1).

pigor: ... o kurcze ma być ... <−1, a ja napisałem wszędzie ... <1 , więc poprawiam powinno być tak : Δ>0 i x_w<−1 i f(−1)>0 ⇔ m²−4*9>0 i −^m₂<−1 i 1−m+9>0 ⇔ ⇔ |m|>6 i −m<−2 i −m+10>0 ⇔ (m<−6 lub m>6) i m>2 i m<10 ⇔ ⇔ 6<m<10 ⇔ m∊(6;10) . ...

Patryk: fajnie ale tylko nie rozumiem tego warunku f(−1)>0

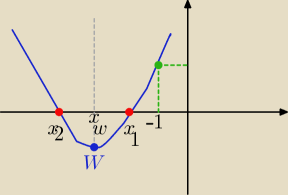
Eta: Δ>0 i x_w < −1 i f(−1) >0

Patryk: o dzięki chyba rozumiem ,dzięki wam

pigor: ... warunek ten tu zapewnia, że przy a=1 >0 , oba pierwiastki leżą po lewej stronie prostej x=−1 , bo gdybyś go nie dał, to mogłoby się zdarzyć , że wierzchołek byłby po lewej stronie x=−1, ale x₁ po prawej , czyli x₁>−1 ( narysuj sobie taki przypadek ...

Krzychu: Funkcja dla x=−1 jest już nad osią OX, czyli, że jest już za miejscami zerowymi. Narysuj sobie szkic i wczuj się w to

Patryk: aha

Patryk: Wyznacz te wartości parametru m, dla których równanie x2+mx+9=0 ma dwa rozwiązania wieksze od 2 Δ>0 X_w>2 f(2)>0 ?

Krzychu: Pytanie do matematyków: dwa rozwiązania koniecznie oznacza, że są to dwa różne rozwiązania co daje nam Δ>0 ?

picia: nie. dwa rozwiazania Δ≥0 dwa rozne rozwiazania Δ>0

pigor: ... powiem tak : dla mnie 2 rozwiązania to 2 różne lub 2 jednakowe, czyli Δ≥0 , ale są tacy, którzy uważają , że 2 rozwiązania to 2 różne (ja z nimi sie nie zgadzam) , czyli Δ>0 i ja tu powyżej dostosowałem się do frakcji tych ... drugich (niech im będzie ).

Krzychu: Pigor: Zadanie: ile rozwiązań ma równanie x⁹⁹=1 odp: ma 99 jednakowych rozwiązań. Trochę dziwnie by było. A pierwiastków ile ma równanie x⁹⁹=1 ? Tak oficjalnie. 99 pierwiastków, czy 1 ?

Basia: jeden w ℛ 99 w ℤ (zespolonych) ale to nie jest dobry przykład ile pierwiastków rzeczywistych ma wielomian W(x) = x² − 2x + 1 ? otóż jeden podwójny, nie dwa

Basia: to jest w gruncie rzeczy dyskusja bez sensu, ale taką nomenklaturę przyjęto w szkolnych podręcznikach, więc się zastosowałam

pigor: ... , jeśli ktoś mówi, że gdy Δ=0 , to ma 1 pierwiastek, wg. mnie mówi bzdety , bowiem jest to jeden pierwiastek podwójny (inaczej − dwa jednakowe − parabola "przykleja się" wierzchołkiem do osi OX − funkcja y=a(x−p)² nie zmienia znaku przechodząc przez p) , natomiast funkcja y=x⁹⁹ jest stopnia nieparzystego i wykres zachowuje się analogicznie do prostej y=ax+b , y=a(x−r)³ itp. funkcji (funkcje tego typu zmieniają znak "przechodząc" przez swoje miejsce zerowe) . dlatego mówię, bez wahania. że równanie twojego typu ma jeden pierwiastek x=1...

Patryk: wiecie jak rozlozyc to na czynniki a⁴+b⁴ ?

Basia: wiemy

Basia: a⁴+b⁴ = (a²+b²)² − 2a²b² = (a²+b²)² − (√2ab)² =................. skończysz sobie ?

Patryk: no postaram się zrobić to samodzielnie dzięki

Patryk: dla jakich wartości parametru m równie x²−(2m−1)x+m²−4=0 ma dwa pierwiastki rzeczywiste mniejsze od 4 ? Δ>0 X_w<4 f(4)>0 dobre zalozenia ?