Całka trefff: całka √1 + ¹_x² dx pierwiastek z jeden dodać jeden przez x do potęgi drugiej

Trivial:

	x2+1		√x2+1
∫√1 + 1/x2dx = ∫√		dx =x>0= ∫		dx = J.
	x2		x

√x²+1 = u x²+1 = u² 2xdx = 2udu / : 2x²

dx		u		u
	=		du =		du
x		x2		u2−1

	u		u2−1+1		du
J = ∫u*		du = ∫		du = u + ∫		= ...
	u2−1		u2−1		u2−1

trefff: dalej tez nie policze nie rozumiem ostatniej linijki tzn licznika u*u = u² − 1 + 1 ? mógłbyś jakoś jasniej to troszke rozpisac?

Mila:

	√x2+1
J=∫√1+1/x2=		dx dla x>0 mnoże licznik i mianownik przez (√x2+1)
	x

	x2+1		x2		1
J=∫		dx=∫		dx+∫		dx=
	x√x2+1		x√x2+1		x√x2+1

	x		1
=∫		dx+∫		dx=
	√x2+1		x√x2+1

	x		U'(x)
J1=∫		dx=√x2+1 ze wzoru ∫		=2√U(x)}
	√x2+1		√U(x)

	1		1
J2=∫		dx teraz podstawienie		=t
	x√x2+1		x

nie wiem, czy trzeba dalej pisać?

trefff: Nie,dzięki wielkie dalej już sobie poradze. Generalnie to takie zadanie miałem 1.Policz objętośc bryły powstałej poprzez obrót wokół osi OX łuku krzywej y=√xe^−x I z tym jakbyś mogła mi jeszcze pomóc to bardzo Cię proszę 2.Oblicz długość łuku krzywej y=ln x 1 ≤x≤4

Mila: cd. całka J₂

1
	=t
x

	1		1
x=		dx=−		dt
	t		t2

	t dt
J2=−∫		=
	t2√1+1/t2

	dt
=−∫		=− ln|t+√t2+1|=
	√t2+1

	1
=−ln|		+√1/x2+1|= dla x>0 po przekształceniach
	x

=−(ln|1+√x²+1|−lnx)=lnx−ln(1+√x²+1) teraz dodaj J₁+J₂ i rozważ przypadek x<0

Mila: Pozostałe zadania pomogę, ale po 22.

trefff: Ok

Mila: objętość : całka nieoznaczona: V=π∫y²dx=π∫(√xe^−x)²dx=π∫xe^−2xdx dokończ Długość łuku: y=f(x)=lnx 4 4 L=∫₁ √1+f '(x)dx=∫₁ √1+1/xdx= licz i pytaj

Krzysiek: długość łuku, to powinno być: (f'(x))² i wychodzi całka do policzenia która już jest policzona

Mila: Dzięki Krzysiek, nic nie widzę w tym edytorze, niedokładnie sprawdziłam . L=∫√1+1/x²dx Krzysiek ustal granice całkowania przy objętości.

Mila: Całkę dla objętości mam obliczoną, ale zostawiam to autorowi zadania.

Krzysiek: granice całkowania dla bryły obrotowej to [0,∞] y=√xe^−x więc dziedzina to: x≥0 e^−x >0 więc y=0 ⇔x=0

Krzysiek: Mila, zauważyłem,że szukasz książki do matematyki dyskretnej (https://matematykaszkolna.pl/forum/151413.html ) być może coś takiego szukasz...http://witmir.pl/ksiegarnia/aspekty-kombinatoryki/3896/

Mila: Dziękuję za informację, aktualnie czytam Grytczuka.

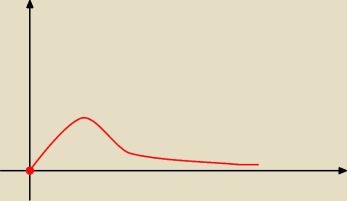
Basia: nie wiem czy to zadanie jest poprawnie sformułowane brak granic całkowania, a to funkcja nie przecina osi OX (OX jest jej asymptotą) więc albo autor nie dopisał, albo chodzi o całkę niewłaściwą od 0 do +∞ wykres tej funkcji wygląda mniej więcej tak jak na rysunku