Oblicz pole figury ograniczonej liniami kaŚka: y=x²−2x−3 y=x+1

Basia: najpierw znajdź punkty wspólne paraboli i prostej czyli rozwiąż równanie x²−2x−3 = x+1 podaj wyniki, potem podpowiem co dalej

kaŚka: po prawo x=−1 , a po normalnie delte liczyć

Basia: nie; wszystko na lewą stronę x² − 2x − 3 − x − 1 = 0 x² − 3x − 4 = 0 i teraz dopiero Δ a tak nawiasem mówiąc (jeżeli to nie jest niedyskretne pytanie) to z jakiego kraju jesteś ?

Mila: x²−3x−4=0 Δ=25 x₁=.. lub x₂=..

Basia: Milu muszę przerwać. Pomożesz Kaśce dalej ?

kaŚka: X1=−1 X2=4

Mila: Pomagam. Dobrze Kasiu.

kaŚka: s=⁻¹∫₄(x²−2x−3)dx − ⁻¹∫₄(x+1)=

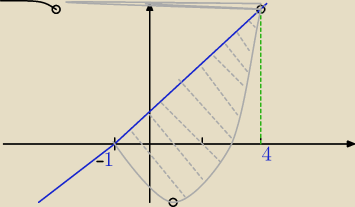
Mila: Liczysz pole obszaru zakreskowanego jako całkę:

Mila: Zobacz co Artur napisał u Kasi, popatrz na rysunek (trochę mi edytor popsuł, ale coś widać). Popraw, bo źle napisałaś.

kaŚka: ? nie wiem to na górze jest źle?

kaŚka: czyli s=⁻¹∫₄(x²−2x−3) − ⁻¹∫₄(x+1)=

Mila: ∫₋₁⁴(x+1−x²+2x+3)dx=∫₋₁⁴(−x²+3x+4)dx= Teraz dokończ

Mila:

	5
Wynik: 20
	6

kaŚka: −∫x²dx+3∫xdx+4∫dx=

x3		3
	+		x2+4x=
3		2

kaŚka: a jak do tego doszłaś

Mila: dobrze:(tylko brak minusa)

	x3		3
F(x)=−		+		x2+4x
	3		2

Teraz policz Pole=F(4)−F(−1)=...

Mila: Artur tak napisał: "wyznaczasz punkty przecięcia się tych funkcji (punkty wspólne) robisz szkic tych funkcji (aby wiedzieć która jest 'nad' którą) i obliczasz ∫ (górna funkcja − dolna funkcja) dx W twoim przykładzie górna funkcja to y=x+1 punkty przecięcia obliczyłaś, to −1, oraz 4 i to są granice całkowania.

kaŚka: wyszło

Mila: To pięknie.

kaŚka: nawet następne sama zrobiłam

kaŚka: y=x³,y=4x wynik mi wyszedł 8

Mila: Zaraz policzę.

Mila: Dobrze, są dwa obszary, pole każdego to 4, razem 8. ( od 0 do 2 i od −2 do 0) Gdzie i co studiujesz?

kaŚka: politechnika łodźka − inżynieria materiałowa ps. możesz mi napisać jak to zrobić x²−x≤y≤√2x też pole

Mila: Punkty przecięcia krzywych: x²−x=√2x x²=x+√2x x²=x+√2*√x x=0 lub x=2 możesz rozwiązać podstawieniem √x=t Pole =∫₀² (√2x−x²+x)dx= 2(?) Jeszcze raz policzę.

Mila: Kasia?

sdasdas: ∊≤πdasdasdassccx