równanie zbioru punktów matem: Napisz równanie zbioru środków wszystkich okręgów zewnętrznie stycznych do okręgu x²+(y−2)² = 1 i stycznych do prostej y = −2.

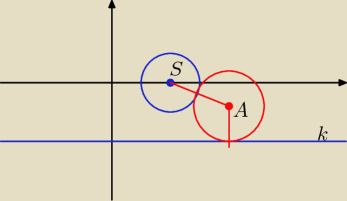
Basia: x²+(y−2)² = 1 to okrąg S(0,2) i r₁ = 1 y = −2 to prosta k równoległa do osi OX k: 0*x + 1*y + 2 = 0 szukam okręgu A(a,b) takiego aby AS = 1+r d(A;k) = r AS = √(a−2)²+(b−0)² = √(a−2)²+b²

	|0*a+1*b+2|		|b+2|
d(A;k) =		=		= |b+2|
	√02+12		1

czyli: √(a−2)²+b² = 1+r |b+2|=r skoro czerwony okrąg ma być styczny do niebieskiego i do prostej ⇒ musi być b> −2 czyli musi być b+2>0 ⇒ |b+2| = b+2 i mamy √(a−2)²+b² = 1+b+2 √(a−2)²+b² = b+3 /()² (a−2)² + b² = b² + 6b + 9 6b+9 = (a−2)² 6b+9 = a²−4a+4 6b = a²−4a−5 b = ¹₆a²−²₃b − ⁵₆ czyli mamy parabolę: y = ¹₆x²−²₃x − ⁵₆

matem: oo bardzo Ci dziękuję!