wartość! lop: Dla jakich wartości parametru p równanie |x− 15| = p³ − 4p ma dwa rozwiązania, których iloczyn jest liczbą dodatnią? p³−4p>0 p(p²−4) p=0 p=2 p=−2 p>0 dla p ∊(−0,2)v(2,+∞) |x−15|=p³−4p x=p³−4p+15 p=−3 −27+12+15=0 (p+3)(p²−3p+5) Δ<0 p=−3 ?

Święty: Jeśli narysujesz wykres funkcji y=|x−15| zobaczysz, że równanie ma dwa rozwiązania, ktorych iloczyn jest liczbą dodatnią, wtedy gdy y>0 i y<15 Dlatego też szukanym parametrem będzie rozwiązanie dwóch nierówności: p³−4p>0 i p³−4p<15

pigor: ... tak , Świety ma rację, a analitycznie możesz do tego dojść np. tak : warunki zadania będą spełnione ⇔ ⇔ p³−4p>0 i x=15±(p³−4p) i (15+(p³−4p))(15−(p³−4p))>0 ⇒ ⇒ p(p−2)(p+2)>0 i 15²−(p³−4p)²>0 ⇔ (*) p∊(−2,0)U(2;+∞) i |p³−4p|<15 ⇒ ⇒ p³−4p<15 ⇔ p³−27−4p+12<0 ⇔ (p−3)(p²+3p+9)−4(p−3)<0 ⇔ (p−3)(p²+3p+5)<0 ⇒ ⇒ p−3<0 , bo ∀_p∊R p²+3p+5>0 ⇔ p<3 ⇒ stąd i z (*) p∊(−2;0)U(2;3) .

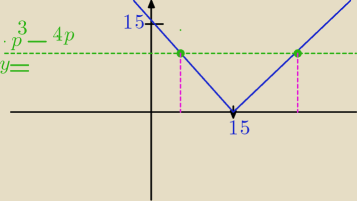
Mila: Szkic i przykład dwóch rozwiązań spełniających warunki zadania.