 Znowuż zadanko z prawdopodobieństwa geometrycznego. Treść:
Odcinek drutu o długości L rozcięto w przypadkowo wziętych dwóch punktach. Obliczyć
prawdopodobieństwo, że z otrzymanych części można zbudować trójkąt.
Moje rozwiązanie:
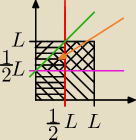
a=x, b=y−x, c=L−y
Stosuję nierówności trójkąta:
Znowuż zadanko z prawdopodobieństwa geometrycznego. Treść:
Odcinek drutu o długości L rozcięto w przypadkowo wziętych dwóch punktach. Obliczyć
prawdopodobieństwo, że z otrzymanych części można zbudować trójkąt.
Moje rozwiązanie:
a=x, b=y−x, c=L−y
Stosuję nierówności trójkąta:
| ⎧ | a+b>c | |
| ⎨ | a+c>b | |
| ⎩ | b+c>a |
| ⎧ | x+y−x>L−y => y>12L | |
| ⎨ | x+L−y>y−x => y<x+12L | |
| ⎩ | y−x+L−y>x => x<12L |
| 18L2 | ||
P(A)= | =18 | |
| L2 |
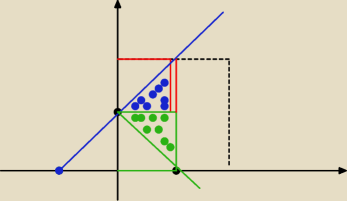
| L | ||
x< | ||
| 2 |
| L | ||
y> | ||
| 2 |
| L | ||
y < x+ | (niebieska prosta) | |
| 2 |
| 1 | ||
i to nam daje | ||
| 8 |
| L | ||
ale to się wszystko dzieje przy założeniu, że a=x< | ||
| 2 |
| L | ||
x< | ||
| 2 |
| L | ||
y< | ||
| 2 |
| L | ||
y > −x + | ||
| 2 |

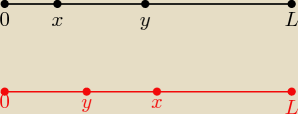 czarne rozważyłeś sam (x<y)
z czerwonego (y<x) będzie ten drugi warunek
czarne rozważyłeś sam (x<y)
z czerwonego (y<x) będzie ten drugi warunek