Prawdopodobieństwo geometryczne student_x: Cześć, znowu mam zadanko z rachunku prawdopodobieństwa. Treść: Z kwadratu jednostkowego wybrano losowo punkt o współrzędnych (x,y) Wyznaczyć funkcję: f(a) = P(min(x,1/2) ≤ a) Za wszelkie wskazówki z góry dzięki!

Jack: zrobiłeś rys?

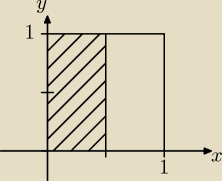
student_x: No właśnie nie... Czy powinien być taki?

Basia: f(a) = 0 dla a≤0 f(a) = 1 dla a≥¹₂ pytanie co dla a∊(0,¹₂) wydaje mi się, że dla a∊(0;¹₂)

	pole prostokąta o bokach a; 1		a
P[min(x;12)≤a] =		=		= a
	pola kwadratu		1

ale pewna nie jestem

student_x: Uff... mi też tak właśnie przed chwilą wyszło (robiłem niezależnie). Mi też tak się wydaje, gdyż właśnie coś takiego było w podobnym przykładzie, który udało mi się odkopać z notatek. Dzięki!