Potęga HELP ME Marek: Zbadaj monotoniczność ciągu an = −(²₃)ⁿ Wiem jak to zbadać ale taki że wiem jak to rozbić ale później nie wiem jak to wszystko obliczyc jak muse potem a_n−1 − a_n zrobić nie wiem jak skracać potegi a_n =−(²₃)ⁿ⁺¹ = −(²ⁿ₃ x ²₃¹) a_n−1−_an = −(²ⁿ₃ x ²₃¹) + (²₃)ⁿ = proszę prosto wytłumaczyć jak sie teraz to skraca

Godzio: Chyba na odwrót:

	2		2		2		2
an − an − 1 = − (		)n + (		)n − 1 = (		)n − 1(−		+ 1) =
	3		3		3		3

	2		1
= (		)n − 1 *		> 0, ciąg rosnący
	3		3

Marek: Skąd 1 się wzięła ?

Godzio: Zobacz co przed nawias wyciągnąłem, właśnie stąd

picia: moze Ci prosciej bedzie jak zrobisz a_n+1−a_n

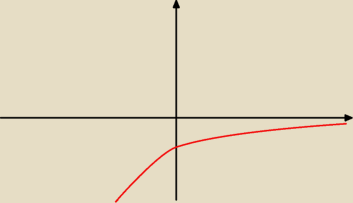
Gustlik: Można skorzystać z własności odpowiedniej funkcji, w tym przypadku wykładniczej:

	2
y=−(		)x i zbadać jej własności dla liczb dodatnich, w tym naturalnych.
	3

	2
Funkcja y=(		)x jest malejąca, bo 0<a<1 (podstawa potęgi), a minus zmienia monotoniczność
	3

	2
na przeciwna, zatem y=−(		)x jest rosnąca, czyli ciąg też jest rosnący.
	3

Na rysunku przybliżony wykres tej funkcji