Liczby zespolone
Marcin: Mam 2 zadania do których nie mam pojęcia jak podejść. Chciałbym żeby ktoś kto to rozumie jakoś
pokazał mi jak się rozwiązuje. Będę bardzo wdzięczny za pomoc.
1. Wykonaj działanie potęgowania posługując się postacią trygonometryczną.
((√3 − 3i)(1+i))2412
2. Rozwiąż poniższe równanie i zaznacz na płaszczyźnie zespolonej wszystkie rozwiązania.
z6 + z4 + z2 + 1 = 0
Mam kilka wersji testów. Treści są te same tylko dane inne. Więc zrozumienie tych zadań
przybliży mnie to zrobienia innych podobnych.
26 cze 21:30
Krzysiek:
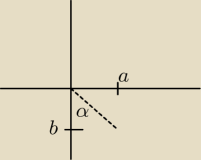
1)
z
1 =
√3−3i
argument z
1 najlepiej z układu współrzędnych odczytać, zaznaczasz punkt z
1 =
√3−3i (a=
√3 ,
| | π | |
b=3) na płaszczyźnie zespolonej i widać, że kąt α= |
| |
| | 6 | |
| | π | | 3π | | 10π | | 5π | |
więc argument z1 wynosi: |
| + |
| = |
| = |
| =φ |
| | 6 | | 2 | | 6 | | 3 | |
|z
1 |=
√(√3)2 +(−3)2
zatem z
1 =|z
1 |(cosφ +isinφ )
spróbuj zamienić z
2 na postać trygonometryczną
(z
1 z
2 )=|z
1 | * |z
2 | (cos(φ
1 +φ
2 ) +isin(φ
1 +φ
2 ))
gdzie 'φ
1 φ
2 " to argumenty z
1 i z
2
aby policzyć potęgę liczby zespolonej skorzystaj ze wzoru de moivre'a
26 cze 22:16
26 cze 22:20
Marcin: Nie rozumiem tego przekształcenia w zadaniu 2. A co do zadania 1 to skąd mam brać z2 ?
27 cze 15:32
Marcin: Dobra wiem już mniej więcej jak liczyć zad 1
27 cze 15:50
Marcin: Wyszło mi tak:
|z1|= 2√3
|z2| = √2
z1 = 2(cos 53π + isin 53π )
z2 = 2 (cos π4 + isin π4 )
podstawiając do (z1 z2) = √24 (cos 1 1/12 π + isin 1 1/12 π) i ten wynik potęgować ?
27 cze 16:37
Krzysiek: potęgujesz zgodnie ze wzorem de moivre'a
(przy cosinusie i sinusie na samym końcu powinno być: 23π/12 jeżeli dobrze policzyłem )
co do pierwszego z dwóch pierwszych czynników wyciągnąłem przed nawias z
4 a potem wyciągnąłem
wspólny wyraz: (z
2 +1)
aby policzyć pierwiastki równania np: z
2 +1=0 korzystamy ze wzoru de Mivre'a:
| | π+2kπ | | π+2kπ | |
z=√−1 =√1*(cosπ +isinπ)=1* (cos |
| +isin |
| ) dla k=0,1 |
| | 2 | | 2 | |
czyli dla k=0 mamy: z=cosπ/2 +isinπ/2 =i
| | 3π | | 3π | |
dla k=1 z=cos |
| +isin |
| =−i |
| | 2 | | 2 | |
27 cze 17:20
Marcin: potęga jest wysoka więc jakie k mam podstawić
? dobrze ci wyszło bo ja to do ułamka
właściwego zrobiłem.
27 cze 18:00
Krzysiek: popatrz na wzór tam nie ma żadnego 'k'...
jeżeli z=|z|(cosφ+isinφ) to:
zn =|z|n (cosnφ +isinnφ)
27 cze 18:04
Marcin: To wynik jest (√24)2414 (cos2412 23π/12 + isin 2412 23π/12)
27 cze 18:11
Marcin: potęga 2412 pomyłka
27 cze 18:11