Prawdopodobieństwo Bogdan: Proszę o pomoc w rozwiązaniu tego zadania Przy okrągłym stole jest sześć numerowanych miejsc. Jest pięć osób biorących udział w imprezie. Są trzy rodzaje runku, a naczynia do picia dwa (białe i czarne). Na ile sposobów można wznieść toast?

konrad: kombinatoryka, nie prawdopodobieństwo to ja sobie pozwolę zaproponować rozwiązanie, choć i tak pewnie będzie źle

6 5
	*53*52

Basia: to chyba nie jest takie proste; stół jest wprawdzie okrągły, ale miejsca są numerowane czyli to, że jest okrągły nie ma praktycznie żadnego znaczenia zakładam, że osoby są rozróżnialne i zakładam, że numer miejsca ma znaczenie (czyli, że co innego toast wznoszony przez A1 i B2, a co innego A2 i B3 na przykład; osoby te same, ale siedzą na innych miejscach) każdej z 5 osób przyporządkowuję jedno z 6 miejsc bez powtórzeń oczywiście, ale kolejność ma znaczenie, bo skoro miejsca są numerowane to A na 1 i B na 2 to nie to samo co B na 1 i A na 2 czyli mamy: 6*5*4*3*2 = 6! sposobów teraz wybieram spośród 5 osób (a właściwie spośród 5 zajętych miejsc) te dwie, które będą

	5 2
wznosić toast czyli

no i razy dwa bo {Ab, Bc} ≠{Ac, Bb}

	5 2		5!
to daje: 6!*		*2 = 6!*		*2 = 6!*4*5 = 20*6!
			2!*3!

tak to widzę, ale mogę się mylić (w założeniach)

konrad: hm, a czy toast musi być tylko pomiędzy dwiema osobami? poza tym nie uwzględniłaś trunków i naczyń

Basia: a faktycznie; to, że są trzy rodzajach trunku przegapiłam to się jeszcze bardziej skomplikuje no skoro są dwa naczynia, to rozumiem, że toast mogą wznieść tylko dwie osoby równocześnie ponieważ mamy trzy rodzajach trunku to jeszcze trzeba pomnożyć przez 3² bo każda z dwóch wznoszących w tym momencie toast może wybrać jeden z trzech (z powtórzeniami)

konrad: co do tych naczyń to ja zrozumiałem tak, że jest x naczyń w dwóch kolorach i każdy może mieć np. białe albo dwóch ma białe, trzech ma czarne

konrad: i nie zgodziłbym się, co rozmieszczenia osób przy stole

Basia: autor napisał: ....trzy rodzaje trunku, a naczynia do picia dwa.... możliwe, że masz rację konradzie, ale wtedy musi być napisane, że: Są trzy rodzaje trunku i dwa rodzaje naczyń........ A poza tym wtedy trzeba by jeszcze wiedzieć ile jest tych naczyń i jakie. Czy tylko 5 np. 2 białe i 3 czarne, albo 4 białe i 1 czarne ? A może 6 lub 7 w różnych konfiguracjach ? A może 5 (lub więcej) białych i 5 (lub więcej) czarnych ? W każdym z tych przypadków będzie inaczej.

Basia: jeżeli miejsca są numerowane, a ludzie rozróżnialni to układ: A1; B2; C3; D4; E5 to co innego niż układ np. A2;B3;C4; D5;E6 ludzie siedzą tak samo, ale mają inne numerki to już jest kwestia interpretacji i określenia czy rozróżniamy przypadki takie, że toast wznoszą te same osoby, siedzące w tej samej konfiguracji, ale na innych miejscach ale skoro podkreślono, że miejsca są numerowane, wydaje się, że tak należałoby myśleć w każdym razie to jest klasyczny przykład niejednoznacznego zadania

konrad: tzn. ja to jeszcze tak rozumiałem, że jest x białych i czarnych naczyń, przy czym każdego koloru jest co najmniej 5 i istotne jest tylko czy dana osoba ma białe czy czarne naczynie, a nie które. Ale to już niema co się teraz na d tym rozwodzić, bo pewnie masz rację.

konrad: jeszcze co do tego rozmieszczenia, to wg Twojego sposobu 2 osoby można by na 3 miejscach rozmieścić na 2! sposobów, co można łatwo sprawdzić, że jest to nieprawdą, wypisując sobie wszystkie możliwości. chyba, że znowu czegoś nierozumiem

Basia: nie na 3*2 = 3*2*1 = 3! i tam też tak liczę: 6*5*4*3*2 = 6*5*4*3*2*1 = 6! (nie 5!)

konrad: sorry, faktycznie

picia: ciekawe co jest do tego picia

Eta: Zakąska

Ajtek: picia

Ajtek: Witam Basia, Eta

Eta: Hej Ajtek

Basia: Witaj Ajtek !

Basia: ale z tymi naczyniami to chyba konrad ma rację; pewnie chodziło o to, że przy każdym miejscu są dwa naczynia

Ajtek: Również w ten sposób bym zinterpretował treść zadania.

konrad: skoro skłaniacie się do mojej wersji, to uwzględniając to co napisała wcześniej Basia, pozwolę sobie zaproponować kolejne rozwiązanie : 61*5³*5²=..

konrad: miało być 6!

konrad: i to przy założeniu, że wszyscy wznoszą toast

Basia: moim zdaniem tak powinno być, tylko to słowo "okrągły" mnie gnębi czy to miał być haczyk ?

konrad: wiesz co, przypomniało mi się właśnie zadanie z kombinatoryki z okrągłym stołem które gdzieś widziałem i coś mi się wydaje, że ktoś w rozwiązaniu tą "okrągłość" uwzględnił

konrad: ale nie interesowałem się tym zadaniem więc nie wiem czy to było słuszne czy nie

Basia: normalnie tak, ale tu jest podkreślone, że miejsca są numerowane i to wszystko psuje narysuję to

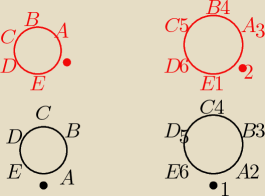
Basia: jeżeli miejsca nie są numerowane to te dwa układy niczym się nie różnią (rysunek lewy) i wtedy się tę "okrągłość" powinno wykorzystać jeżeli są numerowane to te już nie są te same układy (rysunek prawy) i "okrągłość" przestaje mieć jakikolwiek wpływ na liczbę sposobów

Basia: Zadanie: a) na ile sposobów można posadzić 5 osób przy okrągłym stole, tak aby A i B siedziały obok siebie b) na ile sposobów można posadzić 5 osób na ławce, tak aby A i B siedziały obok siebie tutaj będzie różnica, a w tamtym zadaniu nie