Parametr paola: Dla jakich wartości parametru m zbiór rozwiązań nierówności x²−2mx−m+1<0 zawiera się w przedziale (−3,1)

Mickej: HMmm Wierzchołek p musi zawierać się w przedziale i funkcja dla wartosci skrajnych przedziału musi być większa od 0 czyli jedyne warunki konieczne to

	b
p=−
	2a

−3<p<1 f(−3)>0 f(1)>0 tylko to rozwiąż i koniec zadania

nik: a dlaczego nie odwrotnie? tzn. f(−3)≤0 i f(1)≤0

paola: Wielkie dzięki, ale skąd na maturze mam wiedzieć że takie założenia musze zrobic? dlaczego takie nierówności są? Proszę pomóż, bo mi już sie zaczyna wszystko kręcić

Mickej: do nik naszkicuj se wykres to będziesz wiedzieć dlaczego paola dlatego że skoro ramiona skierowane do góry to aby w danym przedziale funkcja była <0 to do tego przedziału musi należeć wierzchołek to oczywiste a te skrajne wartosci to dlatego że skoro ma być mniejsza w tym przedziale to poza przedziałem musi być >0 to najlepiej sobie naszkicować wykres i oblukać to ładnie to będzie widać

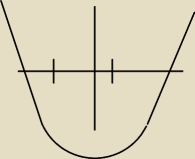
Mickej: wykres funkcji kwadratowej te pionowe kreski to −3 i 1 na osi i już wiadome dlaczego taka nierówność a nie inna

kamil: Mickej a nie powinno byc ze f(−3)0 i f(1)=0

Mickej: nie nie powinno musi być że >0 bo te wartosci już są poza przdziałem

Mickej: ten wykres to jest oczywiscie taki gdyby była inna nierówność ułożona niż założyłem czyli wykres jest błędny chciałem tylko pokazać ze moja nierówność jest konieczna

Krzysiek: (−3,1) to przedział otwarty, więc wszytko co pomiędzy tymi liczbami ma być <0, same te liczby=0, a to co na zewnątrz tego przedziału >0

Mickej: dokładnie o tym mówię od samego początku

paola: Powiem Wam szczerze że ja już nic nie kumam

paola: to wiem co Krzysiek napisał. Rozumiem. Ale czemu liczymy f(x)>0 skoro w treści nic o tym nie ma

paola: nie chodzi w zadaniu o obliczenie wartości wlaśnie w tym przedziale?

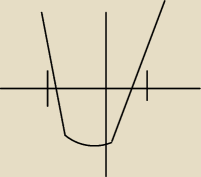
Mickej: no patrz skoro rozwiązanie ma należeć do przedziału(−3;1) i to ma być mniejsze od 0 to logiczne że funkcja dla liczb należących do tego przedziału ma być <0 a dla liczb poza przedziałem >0 bo wykres powinien wyglądać jak ten który narysowałem bardzo prowizorycznie ale dobrze

Krzysiek: Tylko jest jeszcze taka kwestia, czy w tym przedziale mają się znaleźć wszystkie wartości ujemne jakie funkcja przyjmuje, czyli funkcja kwadratowa z miejscami zerowymi w −3 i 1, czy może tych wartości <0 może być więcej poza tym przedziałem, przykładowo funkcja by wtedy miała miejsca zerowe w −10 i 15.

paola: no tak to dlaczego f(−3)>0 a nie f(−3)<0?

Mickej: wzorowe rozwiązanie to te założenia które podałem −3<p<1 f(−3)>0 f(1)>0 nie potrafię tego wytłumaczyć pisząc

Krzysiek: wpiszczie sobie tutaj http://www.jogle.pl/wykresy/ (x+3)(x−1) i zobaczycie jak ma wyglądać wykres.

Krzysiek: czy ja to dobrze rozwiązałem? skoromiejsca zerowe to −3 i 1 to wierzchołek paraboli jest dokładnie pomiędzy tymi punktami, czyli ma pierwszą współrzędną −1, a wiemy, że ta współrzedna

	−b		2m
określa się wzorem		, więć −1=		,
	2a		2

m=−1

paola: odp jest że m∊R

Krzysiek: tylko w tym problem, że jak podstawie to m=−1 to nie wychodzi

Mickej: ale to się ma zawierać w tym przedziale a nie ma tworzyć taki przedział przeczytajcie uważnie treść zadania

Krzysiek: Dobra Mickej, to pokaż może po kolei jak Ty to zrobisz tak, żeby był wynik.

Mickej: ja bym sprawdził najpierw delte ale chciałem wam przekazać jak się takie zadanie powinno robić

Mickej: p=m wierzchołek −3<m<1 f(−3)=18+6m+1>0 m>−19\6 f(1)=2−3m+1>0 m<1 i z delty wynika że m≠1\2 wspólny przedział i po zadaniu

Bogdan: Wskazówka. Jeżeli pierwiastki trójmianu f(x) = ax² + bx + c należą do przedziału (p, q), to należy wziąć pod uwagę następujące założenia: 1. a ≠ 0 2. Δ > 0 3. a * f(p) > 0 4. a * f(q) = 0

	−b
5.		> p
	2a

	−b
6.		< q
	2a

Rozwiązaniem jest część wspólna rozwiązań wszystkich wymienionych założeń.

Mickej: może teraz nie będą zadawać pytań dlaczego

Mickej: 4. a*f(q)>0 chyba powinno być a nie =0

Bogdan: Tak Mickej, z rozpędu wstawiłem znak =, zamiast >. Ma być a*f(q) > 0. Dziękuję

Bogdan: Zadanie maturalne z 2000 r. Długości boków czworokąta, w który można wpisać koło i na którym można opisać koło są równe: a, b, c, d. Udowodnić, że pole P tego czworokąta wyraża się wzorem; P = √abcd.

Bogdan: Przepraszam, wkleję do zadanie do innego wątku.

Krzysiek: "z delty wynika że m≠1\2 " Wszystko już rozgryzłem, tylko tego nie rozumiem? Δ=(−2m)²−4(−m+1)=4m²+4m−4 4m²+4m−4>0, czemu ma z tego wynikać, że m≠1/2?