funkcje -maturalne kamil: dla jakich wartosci parametru m, rownanie Ix−1I=m²−2m+1 ma dwa pierwiastki dodatnie?

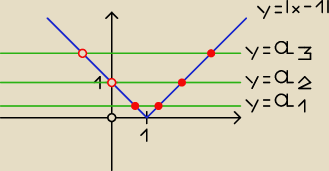
Bogdan: Wykres y = |x − 1| (niebieska linia) jest przecinany przez prostą y = a (zielona linia) w dwóch punktach wtedy, gdy a > 0 Dla a < 0 nie ma punktów wspólnych, dla a = 0 jest 1 punkt wspólny. W podanym zadaniu a = m² − 2m +1. Założenie: m² − 2m +1 ≥ 0 ⇒ (m − 1)² ≥ 0 ⇒ m ∊ℛ (m jest w założeniu dowolną liczbą). Równanie ma dwa rozwiązania dodatnie (czerwone kropki) wtedy, gdy 0 < a < 1, czyli 0 < m² − 2m +1 < 0. Wystarczy rozwiązać tę podwójną nierówność.

kamil: no tak! przy twoim rozwiazaniu zadanie wydaje sie byc proste i oczywiste! dzieki wielkie Bogdanie