funkcja liniowa koko: mam problem z zadaniem: wyznacz zbiór tych punktów płaszczyzny, których współrzędne spełniają układy nierówności:

⎧	|x|+|y|≤3
⎩	|y|≤2

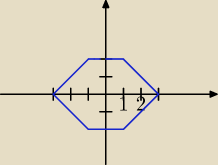
i robię to tak: 1. x+y≤3 y≤3−x 2. −x−y≤3 y≥−3−x 3. y≤2 4. y≥−2 powinno wyjść coś takiego(to w środku sześciokąta), widać, że jest 6 prostych, nie 4 , jakie są dwie pozostałe?

spa: gimbus czytaj książki a nie zakładasz tematy w internecie

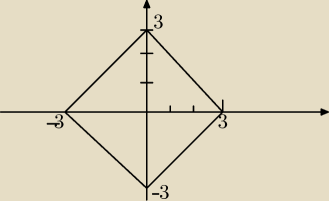
MX: To jest ilustracja równania |x|+|y|=4 To powinno Ci wyjaśnić wątpliwości.

ICSP: MX to jest ilustracja równania |x| + |y| = 3 a nie 4.

Mila: Oczywiście, tak jak potrzeba w zadaniu, to literówka. Autor, chyba się domyślił, jeśli nie, to teraz już jasne.

Grześ: tylko, że to jest jeszcze obszar wewnątrz, czyli nalezy go zamalowac/zakreskowac

koko: nie wiem skąd się biorą te dwie linie ukośne w prawo od −3 do 3

Mila: Rozważamy wyrażenie |x|+|y|≤3 w każdej ćwiartce I Ćwiartka x≥0 i y≥0 x+y≤3 czyli y≤−x+3 II ćwiartka x<0 i y≥0 −x+y≤3 czyli y≤x+3 III ćwiartka x<0 i y<0 −x−y≤3 czyli −x−3≤y inaczej zapisane y≥−x−3 IV ćwiartka x≥0 i y<0 x−y≤3 x−3≤y należy zaznaczyć obszar wewnątrz kwadratu