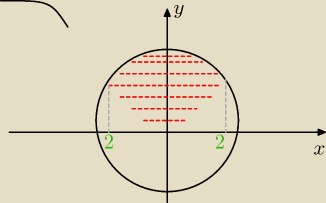
całka oznaczona Kwachu: ∫∫_D dx dy D{x²+y²=8; 2y=x²} całka będzie wyglądała tak? : ₋₂∫² dx _^x22∫^√8−x2 dy czy ₋₂∫² dx _√8−x²∫^x2₂ dy (nie wiem czemu, ale nie chce zaznaczyć mi paraboli na rysunku. obszar wspólny zaznaczyłem czerwonymi kreskami)

Krzysiek: to pierwsze,jak całkujemy po osi 'y' to najpierw 'napotykamy' funkcję y=x²/ 2 a potem równanie koła

Kwachu: kurcze. też tak zrobiłem i pole wyszło mi ujemne. spróbowałem zamienić górę z dołem i pole wyszło dodatnie. zaraz wpiszę jak to policzyłem tą 1 całką i proszę o znalezienie błędów

Krzysiek: http://www.wolframalpha.com/input/?i=integral_%28-2%29%5E%282%29+%28integral_%28x%5E2+%2F2%29%5E%28sqrt%288-x%5E2+%29%29+dy%29dx

Kwachu: −2∫2dx x22∫√8−x2 dy = −2∫2 [y]√8−x2 x22 dx= −{−2}∫2

	x2		2√(8−x2)3		x3		2√43		8
(√8−x2 −		) dx= [		−		]2−2=		−		−
	2		3		6		3		6

	2√43		8		−16
		−		=
	3		6		6

no a pole nie może być ujemne.

Kwachu: wolfram pokazał sam wynik. jak to policzył nie ma

Krzysiek: ale w jaki sposób policzyłeś całkę z ∫√8−x² dx ... na pewno to nie jest to co masz tam później napisane... tą całkę np. przez części u'=1 v=√8−x²

Kwachu: dobra widze gdzie mam źle. tą całkę ∫√8−x² dx zapisałem jako ∫(8−x²)^<span style="font-family:times; margin-left:1px; margin-right:1px">¹₂ dx i

	xa+1
wykorzystalem wzór ∫xa dx=		+ c gdzie tutaj to nie jest samo x... dzięki
	a+1