GEOMETRIA ANALITYCZNA Olaaaaa: Na płaszczyznie obrano pkt A i B , takze A = ( 3 , −2 ) i B = ( 1 , −6) . Napisz rownanie symetralnej p odcinka AB . POMOCYYYY

Olaaaaa: Na płaszczyznie obrano pkt A i B , takze A = ( 3 , −2 ) i B = ( 1 , −6) . Napisz rownanie symetralnej p odcinka AB . POMOCYYYY

123: Symetralna dzieli odcinek pod kątem prostym na pół, czyli trzeba obliczyć prostą prostopadłą do prostej AB i przechodzącej przez środek odcinka AB. Zatem: 1. Liczę równanie prostej AB: −2 = 3a + b −6 = a + b −−−−−−−−−−−−−−− 4 = 2a a = 2 −6 = 2 + b b = −8 y = 2x − 8 2. Liczę środek odcinka AB:

	1 + 3		−6 − 2
SAB = (		;		)
	2		2

	4		−8
SAB = (		;		)
	2		2

S_AB = (2; −4) 3. Liczę równanie symetralnej:

	1
Początkowo prosta ma postać: y = −		x + b
	2

Podstawiam teraz punkt S_AB:

	1
−4 = −		*2 + b
	2

−4 = −1 + b b = 3

	1
Równanie symetralnej ma postać: y = −		x + 3
	2

123: Mały błąd się wkradł tam na samym końcu powinno być b = −3 a nie "3"., zatem równanie ma postać:

	1
y = −		− 3
	2

123: Boże...

	1
y = −		x − 3
	2

Olaaaaa: Yee dziekuje !

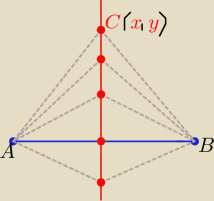
Eta: 2 sposób Z def. symetralnej |CA|= |CB| to |CA|²= |CB|² (x−3)²+(y+2)²= (x−1)²+(y+6)² x²−6x+9+y²+4y+4= x²−2x+1+y²+12y+36 po redukcji 4x+8y+24=0 /:4 x+2y+6=0 −− równanie symetralnej w postaci ogólnej y= −¹₂x−3−−− w postaci kierunkowej

Gustlik: Kochani, czemu Wy proponujecie takie zagmatwane metody? To się robi WEKTORAMI ! A = ( 3 , −2 ) i B = ( 1 , −6) AB^→=[1−3, −6−(−2)]=[−2, −4]

	wy
Z wektora liczę wsp. kierunkowy a=		, gdzie [wx, wy] − współrzędne wektora
	wx

	−4
a=		=2
	−2

Liczę wsp. kierunkowy symetralnej jako prostej prostopadłej:

	1
a2=−
	2

Symetralna ma równanie

	1
y=−		x+b
	2

Liczę srodek odcinka

	3+1		−2−6
S=(		,		)=(2, −4) i podstawiam do równ. symetralnej
	2		2

	1
−4=−		*2+b
	2

−4=−1+b b=−3

	1
Odp: y=−		x−3
	2

To NAJPROSTSZA METODA, nie potrzeba żadnych skomplikowanych układów równań.

krystek: @Gustlik daj sobie spokój z tymi uwagami. Pozdrawiam.

Mateusz: Gustlik w wielu rzeczach sie z tobą zgadzam ale nie zgodze się z jednym że to: −2 = 3a + b −6 = a + b jest skomplikowany układ równań takie układy powinni umieć rozwiazywać gimnazjaliści skomplikowany to moze byc np taki układ równań: { 3x−y+z=6 {x+mz=3 {x+y+3z=6

Eta: Gustlik te twoje uwagi stają się delikatnie mówiąc− "upierdliwe" sorry, daj na luz ! Pozdrawiam

Eta: Twoje

Gustlik: Mateusz, tylko po co rozwiązywać zadania na dwóch niewiadomych, skoro można na jednej? Równanie liniowe czy kwadratowe z jedną niewiadomą jest zawsze łatwiejsze od ukladu z dwiema, poza tym potrzebujemy samego współczynnika kierunkowego AB, całe równanie prostej AB nie jest potrzebne. Eta, Twoja metoda jest dobra, tylko po co uczeń ma męczyć się wzorami skróconego mnożenia, jak może obliczyc współrzędne wektora, co jest banalne i rozwiązać proste równanie liniowe? Poza tym sama mówiłaś, że do geometrii analitycznej potrzebna jest wiedza o wektorach. Ja po prostu chcę Was namówić, żebyście pokazywali krótkie i proste metody, a nie te skomplikowane. Pozdrawiam

Eta: Echh Gustlik jesteś jednak −−− "ciężkim przypadkiem" Napisałam wyraźnie : "2 sposób !

Eta: Kiedyś Cię pytałam, czy masz na imię Wojtek ? Ciągle powtarzasz się ! czyli "wkoło Wojtek"

Gustlik: Eta nie jestem ciężkim przypadkiem, ale u licha pokazujmy przede wszystkim NAJPROSTSZE SPOSOBY, a szczególnie te, których nie omawia się w szkole. Nie gmatwajmy prostych zadań, rozwiązujmy na JEDNEJ niewiadomej, a nie na dwóch czy trzech, o ile się da. Jak będziemy pokazywać długie metody, to następna maturę znów obleje 21 % albo więcej, bo im dłuższa metoda, tym mniej zrozumiala dla uczniów i łatwiej o pomyłkę. A z wektorów w geometrii analitycznej można dużo zrobić, zwłaszcza, ze zdarzaja sie zadania z podpunktami a) wyznacz równanie symetralnej, b) wyznacz równanie wysokości trójkata poprowadzonej z punktu C, c) oblicz pole trójkąta. Jak zaczniemy wektorami np. pkt a) to potem mamy o wiele mniej obliczeń w pktach b) i c), bo wykorzystujemy raz obliczone współrzedne wektorów w pkcie a) i nie musimy robić wszystkich obliczeń od nowa, zyskujemy cenny czas. Nie uczmy uczniów metod "wkoło Wojtek" (słuszne określenie − dobre na tzw. "szkolne" metody, a nie do mnie), a jeżeli juz, to pokazujmy jako ciekawostke, że tak też można. Eta, mam nadzieję, że mnie rozumiesz, zwłaszcza, że zawsze rozwiazywałas krótkimi metodami. Długie metody są dobre, ale dla uczniów z rozszerzeń mat−fiz, a nie dla uczniów z podstaw. Eta ja się Ciebie nie czepiam, ale pokazuj dwa sposoby − najpierw krótki, a potem długi i wszystko będzie OK, uczeń wybierze to, co mu podpasuje. A z doświadczenia wiem, że wektory każdy rozumie. Pozdrawiam

Eta:

Mila: Gustlik, jeżeli chodzi o skorzystanie z wektora (prostopadłego do symetralnej) w tym zadaniu, to ja widzę tak: AB^→=[−2,−4] równanie symetralnej w postaci ogólnej: −2x−4y+C=0 podstawiam wsp. środka odcinka S=(2,−4) −2*2−4*(−4)+C=0 −4+16=−C C=−12 −2x−4y−12=0 2x+4y+12=0 Pozdrawiam wszystkich autorów rozwiązania tego zadania.

pigor: ... i o to tu chodzi ... MIla . cieszę się, że to chyba ja wywołałem na tym forum tak konstruktywne ... rozmowy no i ... rozwiązania

Gustlik: Mila, można, ja niektórym też tak pokazuję. Ale wiecej osób woli rozwiązywać z równania kierunkowego, bo wtedy jest to zwykła funckja liniowa. Poza tym prostopadłość wektora i prostej nie jest pokazywana w szkole nawet na rozszerzeniu, a szkoda. Pozdrawiam

Monika: Gustlik to nie są zagmatwane sposoby .Jak dla mnie łatwiejsze jak Twoje wektory Moze dlatego ze często na lekcjach własnie tymi sposobami rozwiązujemy zadania

gośc: Moim zdaniem ludzi należy uczyć prostoty i elegancji rozwiązania. W tym wypadku najprostszym i eleganckim rozwiązaniem jest rozwiązanie Ety. Gustlik, przez swą miłość do wektorów, nie zauważył, że rozwiązanie za pomoca rachunku wektorowego w tym przypadku jest bardziej skomplikowane −− trzeba liczyć etapy pośrednie −− jakieś środki odcinka −− wsp. kierunkowe itd., itp. W rozwiązaniu Ety równanie prostej mamy natychmiast, po paru (bo nawet nie kilku) elementarnych przekształceniach prostej równości.

Skipper: ... a ja nie rozumiem dlaczego ciągle uciekacie od gotowego wzoru (jest w tablicach) na równanie prostej przez dwa punkty. Po co "wpędzacie" w układ równań lub wektory skoro można podstawić do wzoru.

pigor: ... o tak , bardzo popieram Skippera, nie raz "robię" z tego właśnie równania (wzoru), który można zapisać w kilku postaciach, ale jakoś ten sposób nie ma przebicia wśród nauczycieli , bo "tłuką" − niestety − od gimnazjum po maturę ten z układem równań prostych kierunkowych, z których a, b "wychodzą" często w nieprzyjemnej postaci ; a co do wektorów , to wcale nie musimy o nich mówić , bo właśnie z klasycznej (nie wiem dlaczego też się o niej też nie mówi) postaci równania prostej przez 1 punkt : y−y₁=a (x−x₁) płynnie możemy przejść do równania prostej przez 2 punkty

	y2−y1		y2−y1
y−y1=		(x−x1), gdzie a=		=tgα jako stosunek
	x2−x1		x2−x1

odległości rzędnych do odległości odciętych danych punktów , a na koniec plusem korzystania z tego wzoru jest jeszcze to, że z tego równania łatwo sprawdzić współliniowość 3−ech danych punktów wstawiając za (x,y) ten 3−ci punkt . ...

Skipper: ... pigor słusznie podkreślił, że ... jeśli nie pytają o równanie prostej a potrzebujemy jedynie współczynnik kierunkowy... to wystarczy "element" tego wzoru

gośc: OK Skipper & pigor −− po części się z wami zgadzam, ale jest jeden problem −− i to jest problem całej polskiej edukacji matematycznej: wrypać kupę wzorów i tylko podstawiać. Dostajemy w efekcie ludzi, którzy nie potrafią myśleć nad rozwiązaniem problemu −− czego przykłady mamy na tym forum −− pytający oczekują od nas konkretnego wzoru lub wręcz rozwiązania. Są kraje, gdzie nie uczy się np. wzorów na pierwiastki równania kwadratowego, tylko umiejętności przekształcania tego równania tak, aby te pierwiastki znaleźć lub nie. Nie powiem, wzory sa przydatne, ale jeszcze lepiej, gdy delikwent radzi sobie bez nich, wychodząc od prostych obserwacji.

Gustlik: Ipgor, tylko że ten wzór jest długi jak trasa Warszawa−Lizbona i ciężko strawny. Natomiast z wektorów mozna obliczyć wiele rzeczy, o czym pisałem, często zdarza się, że raz obliczony wektor wykorzystujemy kilka razy i jest DUŻO ŁATWIEJ. Wektory są najprosztszą metodą na tego typu zadania.

Skipper: ... Ty Gustlik chyba sam nie czytasz tego co piszesz. Jeśli problemem jest zdanie matury ... to cóż jest prostszego niżeli wykorzystać wzór, który jest w tablicach. Jeśli problemem jest długość wzoru to po to są tablice ... Ale oczywiście specjalnie to upraszczam ... pigor skutecznie wywiódł jak prosto "wyprowadzić" ten wzór ... średnio myślący ... nie może mieć z tym problemu.

	y2−y1
Jaki problem można mieć w zrozumieniu, że a=tgα=
	x2−x1

( na rysunek szkoda nawet czasu) ... a wzór y=ax+b zna chyba każdy.

pigor: . zgadzam się i z cieszę się , że nie jestem w tym co mówisz gosciu ... osamotniony, a na to forum wpadam od niedawna i próbuję to wprowadzać w praktyce co chyba już nie jest takim zaskoczeniem jak było na początku , bo twierdzę ,że "mądry" użytkownik jest na tyle elastyczny, że weźmie z tego co będzie uważał za fajne,a to już będzie dużo p.s. co do pierwiastków to poszedłbym dalej i np. za niekorzystanie z "delty" promowałbym ucznia np. 1 punktem więcej lub czymś w tym rodzaju, aż stałaby się marginesem w polskiej szkole , czego sobie i innym życzę . ...

Eta: I w nagrodę dla Was Panowie Pozdrawiam

Skipper: ... w tych "swoich" skąd inąd fajnych wektorach liczy w_x jako x₂−x₁ ... w_y jako y₂−y₁

	wy
potem a jako		... i z uporem maniaka "wkoło Wojtek" − ... że to niby coś innego
	wx

i coś prostszego.

Eta: Jeżeli A( −3, 12) i B( 1, 12) to bez wektorów AB: y= y_A= y_B= 12 odp: AB: y=12 podobnie: A(−5,36) B(−5, −19) to AB: x= x_A= x_B odp: AB: x= −5

pigor: ..no właśnie Drogi Gustliku naprawdę ten twój sposób tu nie potrzebuje wektorów, przecież twoje składowe wektorów, to "moje" różnice we współczynniku a (wystarczy do tego Δ prostokątny w układzie xOy i te dane 2 punkty, przy okazji wyprowadzania wzoru na a i potem go tylko stosować ) , więc po co je najpierw liczysz i dopiero potem wstawiasz do a , kiedy możesz od razu liczyć po prostu długości przyprostokątnych i nie nazywać ich współrzędnymi (ja nazywam składowymi) wektora we wzorze na ten współczynnik a=tgα=^y_x , pozdrawiam . ...

Eta: Dokładnie Nic nie poradzimy,że Gustlik jest miłośnikiem wektorów

pigor: ... ufff chyba wyjaśniliśmy sobie wszystko, a więc ... róbmy swoje i może coś nieco mniej lub więcej, lub może ... inaczej, a wnioski niech wyciągają (a więc myślą z czego może nawet nie zdają sobie sprawy) ci co naprawdę zechcą zrozumieć to , o co proszą , a my i nie tylko my, przecież chcemy im w tym pomóc z własnej, nie wymuszonej woli, bo to lubimy , prawda ? Eta dzięki , jesteś naszą Panią . ...

Skipper: ... ale Gustlika też lubimy − jeno troszkę inaczej − Mam nadzieję, że On nas też −

Gustlik: Ja Was lubię i nie inaczej tylko normalnie, niemniej chcę pokazywać proste i rzadko stosowane w szkołach metody, a do tych metod nalezą wektory. Ja po prostu jestem miłośnikiem prostych i szybkich metod i tych uczę. A wektorów uczę po to, że uczeń później jak widzie dane typu =(1, 2) i B=(3, 4) to wie, że trzeba zacząć od wektora i resztę liczyć z wektora. Po prostu ujednolicona metoda, a z wektorów mozna obliczyć i współczynnik kierunkowy i długość odcinka i pole trojkąta, można zbadać prostopadłość prostych, np. boków trójkąta i udowodnić, że trójkąt jest prostokątny itp. Często obliczenie wektora ułatwia rozwiazanie kilku podpunktów w zadaniu, bez konieczności wracania się do początku. Dlatego uczę wektorów, bo to PODSTAWA geometrii analitycznej.

Saizou : Po przeczytaniu tematu, stwierdzam że nie warto się kłócić co jest najlepszym sposobem na rozwiązywanie zadań, bo to zależy od danej osoby, kto co lepiej rozumie. Np. Ktoś nie lubi wektorów i unika ich jak ognia, ale np. przypadło mu do gustu np. rozwiązanie Ety. Według mnie ważne jest żeby pokazywać różne sposoby liczenia, ale to autor zadania decyduje, które rozwiązanie jest najlepsze dla niego.

Eta:

Mateusz: Tak warto też jezeli juz stosujemy jakieś wzory ktore uczen widzi np pierwszy raz warto pokazać skąd sie wzieły np wzor na wspołczynnik kierunkowy prostej−bo jest to forma utrwalenia dla ucznia/maturzysty chociaz zdaje sobie sprawe ze nie wszystko da się ładnie wyprowadzic bez np stosowania wyzszej matematyki ale co sie da to warto bo jaki sens jest kuć na pamiec wzór ktory nie wiadomo skad sie wziął(dla ucznia) kiedy w stresie maturzysta zapomni go i nici z liczenia np wspołczynnika kierunkowego czy pola trójkąta z wyznacznika lub co gorsza pomiesza dane i klops jeszcze większy dlatego proponuje tak właśnie i nie robić od razu raban że to jest krótszy sposób czy lepszy tylko pokazać alternatywe jak np tutaj: https://matematykaszkolna.pl/forum/150978.html picia zrobił typowo układem równań ok ja zrobiłem inaczej a pigor jeszcze krócej i jezeli uczennica jest ambitna to przeanalizuje te sposoby i czegoś się też nauczy .

pigor: ... i właśnie mi o to chodzi, co mądrze icia , udzielający krótkich, ale treściwych podpowiedzi, wskazówek w swoich postach , naszą dyskusję podsumował ; dziękuję , . ...

pigor: ... nie icia , przepraszam , tylko omiało być picia

picia: wtrace tylko ze w zadaniu z ciagami nie liczylem z typowego ukladu rownan

Mateusz: To też fakt

pigor: ... picia ja czułem, że coś nie tak z tobą w tym zadaniu z ciągiem , ale tobie nie trzeba nic tłumaczyć , a ja właśnie swoje rozwiązania "robię" dla takich jak ty , pozdrawiam . ...

Gustlik: Picia zrobił tą samą metodą, którą ja robię, czyli krótszą i łatwiejszą. Pozdrawiam.

Bezimienny: Im więcej metod tym lepiej.

Eta: http://a8.sphotos.ak.fbcdn.net/hphotos-ak-ash3/577217_369632079744606_333316346709513_988521_493341671_n.jpg

Monika: Eta dobre haha

Mateusz: No Gustlik idąc twoim tokiem spierałbym sie czy jest to prostsza metoda a czy na pewno krótsza

Eta:

Gustlik: Mateusz − krótsza i prostsza − przede wszystkim masz dwa równania ale z JEDNĄ niewiadoma, a nie układ. Wystarczy zapamiętać zasadę, że od wyrazu o wyższym numerze odejmujemy wyraz o niższym numerze, a różnica numerów to ilość "r"−ów, np. a₉−a₆=3r, a₈−a₃=5r itp... I mamy równanie z JEDNĄ niewiadomą r. Obliczamy r, a potem obliczamy wyraz a₁ np. gdy mamy dane a₃ i a₈, to ja wybieram wyraz leżący "bliżej" a₁, czyli liczę z a₃, a więc a₁=a₃−2r, "cofam się" o 2 wyrazy, r już znam więc znów mam JEDNĄ niewiadomą − a₁. To jest mniej więcej tak, jakbym wsiadł do pociągu na stacji nr 3 i jechał na stację nr 1 − cofam się o 2 stacje. Metoda "podjedź − cofnij". Gdy trzeba obliczyc wyraz o wyższym numerze − to "podjeżdżamy" do przodu, np. a₈=a₅+3r (wsiadamy na stacji 5 i jedziemy pociągiem na stację 8, czyli podjeżdżamy o 3 stacje), a jak chcemy obliczyć wyraz o niższym numerze − to "cofamy się", np. a₂=a₆−4r (wsiadamy na stacji 6 i jedziemy na stację 2 − o 4 stacje do tyłu). Podjeżdżasz − dodajesz "r"−y, cofasz się − odejmujesz "r"−y.

Mateusz: Gustliku mi tego nie musisz tłumaczyć bo ja wiem o co w tym chodzi tyle ze moja metoda tez nie jest zła wystarczy zapamiętać prosto wyprowadzony wzor na r gdy mamy podane dwa różne wyrazyciągu i niemal w pamieci juz mamy policzone r(nie traci sie miejsca na kartce ) i potem tylko szybciorem jedno równanie i mamy własnie np a₁ i r Pozdrawiam.

Gustlik: Monika, na lekcji większość zadań robi się zagmatwanymi mitodami. Pytam więc: po co stosować uklad równań, tam gdzie wystarczy jedna niewiadoma? Poza tym zdarzają sie zadania z geometrii analitycznej z kilkoma podpunktami, np. a) oblicz długość odcinka AB, b) wyznacz równanie wysokości trókąta opuszczonej z wierzchołka C, c) oblicz pole trójkata. Licząc z wektorów jest o wiele prościej, bo z raz obliczonych współrzędnych wektorów zrobisz użytek we wszystkich trzech podpunktach. Bez wektorów cofasz się za każdym razem do początku i liczysz takie zadanie duuużo dłużej. Dlatego ja uczę na wektorach, bo one są proste i wiele można za ich pomocą obliczyć w szybki i łatwy sposób.

Saraa: Jak obliczyć symetralną odcinka