Proszę, kto mógłby pomóc? Sandra: Oblicz pole trójkąta, którego dwa boki mają długości 8 i 5, a środkowa poprowadzona do trzeciego boku ma długość 6.

krzy: a²*b²=c² 6²*b²=5² 36* b² = 25 b²=36−25 √11

kkk: rys

kkk: P= a*h/2

Eta: 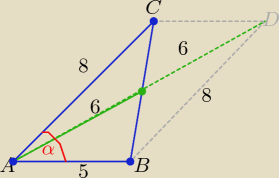1 sposób ( jak na rys) Czworokąt ABCD jest równoległobokiem P(ΔABC)= P(ΔABD)

	12+5+8		25
ze wzoru Herona P= √p(p−12)*(p−8)*(p−5) , p=		=
	2		2

	25		1		9		15		15√15
P= √		*		*		*		= ........... =
	2		2		2		2		4

2 sposób

	1
P(ΔABC)=		*8*5*sinα
	2

	1
długość dwusiecznej : d=		√2a2+2b2−c2 a= 8 , b= 5 c= |BC|
	2

( 2d)²= 2a²+2b²−c² po podstawieniu danych 144= 128+50 −c² ⇒ c²= 43

	a2+b2−c2		11
cosα=		= ...... =
	2ab		16

	√135		3√15
sinα= √1−cos2α=		=
	256		16

	1		3√15		15√15
P(ΔABC)=		*8*5*		=
	2		16		4

Eta: Gustlik a tu , którą metodę wybierasz? Oczywiście,że można też wektorami.

Gustlik: To nie geometria analityczna więc wektorami byłoby ciężko. Wybieram I sposób − ze wzoru Herona, bo łatwiejszy, a wzór Herona to tez jedna z moich ulubionych metod.

Mila: Dobranoc, przyjemnych snów.