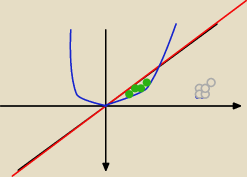
wyznaczanie obszaru całki gradient: Obszar D (zielony) ograniczony y=x² na niebiesko i y=x na czerwono zapiszemy jako P ∫₀¹ [x − x²] dx

gradient: pomocy

Kwachu: x²=x x=0 x=1 ₀∫¹ x dx − ₀∫¹ x² dx=*

	x2		x3
∫ x dx=		∫x2 dx=
	2		3

	1		1		3		2		1
*=		−(		)=		−		=
	2		3		6		6		6

chyba tak

gradient: Mi też wyszło 1/6

Kwachu: ciesze się razem z tobą

gradient: Teraz muszę pojąć jak sprawdzić czy obszar D jest normalny względem osi X... hmmm....

Kwachu: nie pomogę. nie wiem co to jest "obszar normalny"

gradient: http://pl.wikipedia.org/wiki/Obszar_normalny A na innym forum matematycznym znalazłam wyjaśnienie, że "Jeśli masz pewien obszar, w którym jego dolna linia ograniczająca jest określona jedną funkcją i jego górna linia jest określonajedną funkcją, to jest on normalny względem osi x. Jeśli te dwa warunki nie są spełnione jednocześnie (np. uskoki, nieciągłość linii), to obszar nie jest normalny względem osi x " więc na logike, mój jest?

gradient: up

gradient: Nikt nic nie wie o obszarze normalnym wzgledem osi x? Jak sprawdzic?

gradient: Czy obszar zaznaczony na zielono moge zapisać jako 0≤x≤1 x²≤y≤x ?