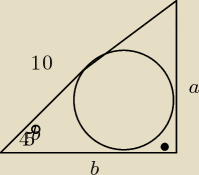
okręgi, proszę o pomoc, bo nie rozumiem. mamma mia: zad1 Na okręgu opisano trójkąt prostokątny o przeciwprostokątnej długości 10 cm. Oblicz długości trójkata i jego pole. zad2 Stosunek długości trójkąta prostokątnego jest równy 3 do 4. Promień okręgu opisanego na trójkącie ma długość 10 cm. Oblicz pole tego trójkąta.

Buuu: 1) Jeżeli dwie styczne przecinają się w jakimś punkcie to długość stycznych pomiędzy tym punktem, a punktem styczności jest taka sama. W naszym przypadku implikuje to trójkąt równoramienny o kącie miedzy ramionami 90^o, a co za tym idzie kąty przy podstawie sa takie same: po 45^o. Mamy więc trójkąt 45−90−45 o przeciwprostokątnej 10. Dalej powinnaś sobie poradzić. 2) Przeciwprostokątna ma zatem 20cm. Pitagoras rzecze: (3x)² + (4x)² = 20² ...

mamma mia: Dziękuję.

AS: Nie bardzo rozumiem wywodów dotyczącego pierwszego zadania. Oznaczając długości przyprostokątnych przez x i y otrzymujemy związek x² + y² = 100. Istnieje wiele par liczbowych (x,y) spełniających to równanie i w każdy z tych trójkątów można wpisać okrąg. Przecież promień okręgu nie jest ustalony,. Istnieje wiele rozwiązań.

picia: podbijam

picia: moze ktos zerknac na to zad.1?

Kwachu: b/10=cos45◯ a/10=sin45◯ chyba tak

picia: a skad wiadomo ze to trojkat rownoramienny? zgadzam sie tutaj z As i tak samo nie rozumiem tych wczesniejszych wywodow

picia: eee tam, jak on by byl rownoramienny to nawet nie trzeba korzystac z f trygometrycznych tylko wysarczy z wlasnosci ekierki moim zdaniem czegos brakuje w tresci.