funkcja logarytmiczna babyclon: W prostokątnym układzie współrzędnych zaznacz zbiór tych punktów płaszczyzny, których współrzędne spełniają poniższe warunki: (rysunek wykonam sama, proszę tylko o wskazanie sposobu rozwiązania)

	xy
a) log2		− log2x * log2y = 0
	2

zał: x, y >0 b) log_y+1(x² − x) > log²_y+1(x² − x), gdzie y∊ (−1,0) zał: x∊(−∞, 0) suma (1,∞)

babyclon:

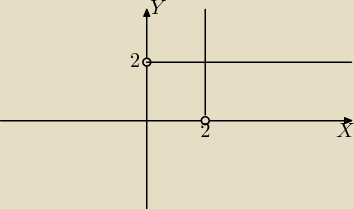
Mila: a) log₂(xy)−log₂2−log₂x*log₂y=0 i x>0 i y>0 log₂x+log_y−1−log₂x*log₂y=0 grupuję wyrazy( 1i ostatni) log_x*(1−log₂y)+log₂y−1=0 log_x*(1−log₂y)−(−log₂y+1)=0 wyłączam (1−log₂y) (1−log₂y)*(log_x−1)=0 (1−log₂y)=0 lub (log_x−1)=0 log₂x=1 lub log₂x=0 x=2 lub y=2 i x>0 i y>0

Mila: b) log_y+1(x² − x) > log²_y+1(x² − x), gdzie y∊ (−1,0) log_y+1(x² − x) − log²_y+1(x² − x)>0 log_y+1(x² − x)*(1−log_y+1(x² − x))>0 x∊(−∞, 0) suma (1,∞) i y∊ (−1,0) rozwiąż ten warunek, podstawa: 0<y+1<1