prawdopodobienstwo naiwna: Dwoje internautów umówiło się na spotkanie w sieci między godziną 17 a 18, przy czym ze względu na koszty połączenia będą na siebie czekać co najwyżej 10 minut i nie dłużej niż do godziny 18. Jakie jest prawdopodobieństwo tego, że się spotkają?

Artur_z_miasta_Neptuna:

	4		2
a) Internauta 1 wchodzi w godzinach 17.10 − 17.50 z prawdopodobieństwem		=
	6		3

jaka jest szansa, że internauta 2 wyjdzie w przedziale 'wejście int. 1 ⁺/₋ 10min czyli w

	1
oknie 20min? oczywiście
	3

	2		1		2
A więc dla przypadku (a) mamy		*		=
	3		3		9

	2
b) internauta 1 wchodzi w godzinach 17.00−17.10 lub 17.50−18.00 z prawdopodobieństwem		=
	6

	1
	3

jakie będzie 'średnie' okno w jakim internauta 2 może się 'wstrzelić? oczywiście będzie to

	0min + 10min
10min +		= 15min
	2

	1
jaka jest szansa, że internauta 2 wyjdzie w przedziale 15min? oczywiście
	4

	1		1		1
A więc w przypadku (b) mamy		*		=
	3		4		12

Ostatecznie:

	2		1
P(A) =		+		= ....
	9		12

naiwna: dziekuje jednak nie rozumiem o co chodzi z tym 15min i "wstrzeleniem w okno". Moglbys wyjasnic

naiwna: prosze : )

Artur_z_miasta_Neptuna: 'wstrzelenie w okno' czyli ... niech geniek wejdzie do neta nie później niż 10min po tym jak zenek się zalogował lub nie wcześniej jak 10min przed tym jak zenek się zalogował jeżeli zenek loguje się zbyt wczesnie 17 lub blisko 18 to geniek ma 'mniejsze okno' Przykład. Zenek loguje się o 17.05 A więc, aby doszło do spotkania to Geniek musiałby się zalogować gdzies pomiedzy 17.00 − 17.15. Przykład 2. Zenek loguje się o 17.02 A więc, aby doszło do spotkania to Geniek musiałby się zalogować gdzies pomiedzy 17.00 − 17.12 Zenek − internauta 1 Geniek − internauta 2

naiwna:

	0min+10min
ok, rozumiem ale nadal nie wiem skad wzielo sie 10min +		, no bo ok 10min ma
	2

zeby sie wstrzelic.. ale skad pozniej to 0..?i czemu tylko raz dzielimy na dwa? mozna by popatrzyc na to tak,ze przed 17 nie moze sie wstrzelic..bo od 17 sie umawiali wiec faktycznie 0, pozniej ma 10 min, potem znow 10min przy 18 no i po 18 znow 0. ale to ja bym inaczej zapisala

Artur_z_miasta_Neptuna: dlaczego w przypadku (b) 'średnie okno' wynosi 15 min? Juz wyjasniam Zenek loguje się gdzieś pomiędzy 17.00 a 17.10 będzie czekał 10min. A o ile wczesniej Geniek mógł się zalogować? (zakładamy, ze 17.00 to najwcześniejsza pora) gdzieś pomiędzy 17.00 a momentem zalogowania Zenka ... jaki będzie ŚREDNIA dlugość tego przedziału? 5min ... dlaczego? Ponieważ: Zenek loguje się o 17.00 to przedział PRZED jego logowaniem wynosi 0min Zenek loguje się o 17.01 to przedział PRZED jego logowaniem wynosi 1min ....... Zenek loguje się o 17.09 to przedział PRZED jego logowaniem wynosi 9min Zenek loguje się o 17.10 to przedział PRZED jego logowaniem wynosi 10min przedziały te tworzą ciąg arytmetyczny = średni element to średnia arytmetyczna maksymalnego i

	0min + 10min
minimalnego elementu i stąd		= 5min
	2

analogicznie dla wejść Zenka w godzinach 17.50−18.00

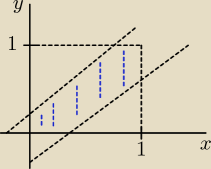
Krzysiek: lub standardowo liczyć: x∊[0,1] y∊[0,1] |x−y|<1/6 − różnica przyjścia jest mniejsza niż 1/6 godziny P(A) to pole zakreskowane na niebiesko

Artur_z_miasta_Neptuna: oczywiście 'czas' nie jest liczony z dokładnościa co do minuty ... ale i tak średnie 'okno' będzie wynosić 10min + 5min = 15min

naiwna: czyli w przypadku 17.50−18.00 jest U{10min+10min]{2}? bo moze sie zalogowac juz o 17.40 i akurat sie "spotkaja" o 17.50 ?

naiwna: i jak to obliczyc Twoim sposobem Krzysiek

naiwna:

Krzysiek: internauta 1 jak i internauta 2 mogą przyjść na spotkanie od 17 do 18 czyli mają całą godzinę zatem: x,y∊[0,1] aby doszło do spotkania różnica ich przyjścia musi być mniejsza od 1/6 godziny i w zależności kto przyszedłby pierwszy tą zależność opisuje moduł, |x−y|<1/6 Ω={(x,y): x,y∊[0,1] } A={(x,y): |x−y|<1/6}

	μ(A)
i teraz P(A)=
	μ(Ω)

μ−miara (pole ) μ(Ω)=1*1 =1 (pole kwadratu) więc musisz policzyć pole tego zakreskowanego obszaru

naiwna: haha, wszystko fajnie i dziekuje za wyjasnienie, tylko jak obliczyc to pole? bo to tu jest u mnie problem

Krzysiek: możesz policzyć pola tych trójkątów i odjąć od pola kwadratu...