Twierdzenie cosinusów... nati: 1) W trójkącie równoramiennym ABC miara kąta przy podstawie jest równa 30^o, a suma wysokości i długości ramienia trójkąta wynosi 16cm. Oblicz pole tego trójkąta. 2) Wykaż, że jeśli w trójkącie o kątach α, β, γ zachodzi związek sinα / 2sinβ = cosγ, to trójkąt jest równoramienny.

sushi_ gg6397228: a) sin α= ... h+b=16 (h−wysokosc, b−ramie) układ równan i po sprawie

Basia: ad.b α = 180 − (β+γ) sinα = sin[180 − (β+γ)] = sin(β+γ) = sinβ*cosγ + sinγ*cosβ czyli mamy

sinβ*cosγ + sinγ*cosβ
	= cosγ
2sinβ

sinβ*cosγ + sinγ*cosβ = 2sinβ*cosγ sinγ*cosβ = sinβ*cosγ sinγ*cosβ − sinβ*cosγ = 0 sin(γ−β) = 0 ⇔ γ−β = 0 ⇔ y = β c.b.d.u.

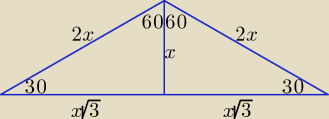
Bogdan: 1) Można skorzystać z własności trójkąta prostokątnego, którego miary kątów ostrych są równe 30^o i 60^o.. x + 2x = 16 ⇒ x = ... Pole P = x*x√3 = ...