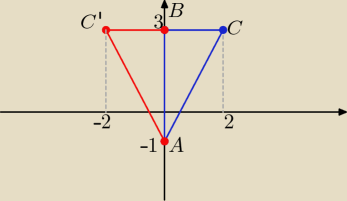
Przystawanie figur weronika: Proszę o pomoc w dwóch zadankach 1. Udowodnij następujące twierdzenia: b) trójkąty o wierzchołkach A=(0,−1), B=(0,3), C=(2,3) oraz A=(0,−1), B=(0,3), C'=(−2,3) są przystające. 2. Dwa przystające trójkąty są wpisane w ten sam okrąg. Udowodnij, że jeden z nich można przekształcić na drugi przez symetrię osiową albo przez obrót. z góry dziękuję

weronika: Pomocy!

Eta: 1/ policz długości boków i z cechy (bbb) trójkąty są przystające

weronika: mi nie wyszło że są przystające nie wiem czemu

weronika: nie wiem czy źle rysunek zrobiłam czy co. Jak ci to wyszło?

Artur z miasta Neptuna: weronika −−− przecież na pierwszyrzut oka widać że są przystające ... mają dwa takie same punkty różnią się tylko C ... które są wzajemnie symetryczne względem osi OX. Są to identyczne trójkąty −−− symetria względem osi OX.

Artur z miasta Neptuna: tfu ... zamiast OX wszędzie tam ma być OY

weronika: ale przecież C'B nie jest równy CB

Eta:

Eta: |CB|= 2 i |C^'B|= 2

weronika: aha jaka jestem głupia pomyliłam osie nie wiem jak ja to zrobiłam źle zaznaczyłam punkt B

weronika: teraz juz kapuje dzięki

weronika: a to drugie zadanie jak zrobić, jak to udowodnić

weronika: nie mam jakoś pomysłu

weronika: wie ktoś jak to zrobić

weronika: proszę niech ktoś pomoże albo chociaż coś podpowie