pomoc pomoc bumblebee: wyznacz zbior wartosci funkji f okreslonej wzorem f(x)=√log cos2πx

Mickej: zauważ że cos2πx przyjmuje maks wartość =1 a min=0 bo minusowa odpada

Mickej: w sumie to jest coś dziwnego bo to sie nie da

imię lub nick: co jest w podstawie logarytmu?

zajkoś: zior wartosci to {0}

bumblebee: mam w odpowiedziach ze zbiorem wartosci jest {0}, zajkoś jak to wyliczyłes

bumblebee: to jest logarytm dziesietny czyli 10 jest w podstawie

Mickej: bo 10⁰=1 i tylko dla jedynki wartość logarytmu nie będzie ujemna

bumblebee: narysowalem wykres tego programem to wygladal tak ze byly to kropki, punkty o wspolrzedneych (x,0), x nalezal do calkowitych

Mickej: dlatego taki wykres bo 2π=360 a cos360=1 a jak x jest całkowity to wiadome że wartość cos bedzie =1

Bogdan: Dzień dobry. Wyznaczmy najpierw dziedzinę funkcji. Założenia: 1. log cos2πx ≥ 0 => log cos2πx ≥ log1 => cos2πx ≥ 1 => cos2πx = 1 2πx = k*2π => x = k, k ∊ C

	−π		π
2. cos2πx > 0 =>		+ k*2π < 2πx <		+ k*2π
	2		2

	−1		−1
		+ k < x <		+ k
	4		4

Z założeń 1. i 2. otrzymujemy D_f = C (zbiór liczb całkowitych).

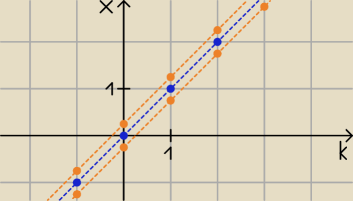
	1
Ilustracją założeń są punkty na prostych: x = k +		(górna pomarańczowa linia),
	4

	−1
x = k +		(dolna pomarańczowa linia), x = k (środkowa niebieska linia).
	4

Dziedziną są liczby całkowite przypisane niebieskim kropkom. Określamy teraz ZW_f − zbiór wartości funkcji f(x). dla x = k ∊ C: cos(k*2π) = 1, log1 = 0, √0 = 0 f(x = k) = √log(cos(k*2π)) = 0 ZW_f: y ∊ {0}