FUNKCJA KWADRATOWA Darnokxxx: USTAL, DLA JAKICH WARTOŚCI parametru "m" jeden pierwiastek równania x²+2mx+2m−1=0 jest większy od 3, a drugi mniejszy od 3

Basia: Δ = (2m)² − 4*1(2m−1) = 4m² − 8m + 4 = 4(m²−2m+1) = 4(m−1)² Δ>0 ⇔ m−1≠0 ⇔ m≠1 √Δ = 2|m−1| czyli dla m>1 mamy √Δ = 2(m−1)

	−2m−2(m−1)		−4m+2
x1 =		=		= −2m+1
	2		2

	−2m+2(m−1)
x2 =		= −1
	2

czyli musi być x₁>3 czyli −2m+1 > 3 −2m > 2 m < −1 sprzeczność bo był badany przypadek m>1 dla m<1 mamy √Δ = −2(m−1) = −2m+2

	−2m+2m−2
x1 =		= −1
	2

	−2m−2m+2
x2 =		= −2m+1
	2

czyli musi być x₁>3 czyli −2m+1 > 3 −2m > 2 m < −1 i to jest odpowiedź do zadania

Darnokxxx: Dziękuje

pigor: ... niech f(x)=x²+2mx+2m−1 , to warunki zadania spełnia układ nierówności : Δ=4m²−4(2m−1)>0 i f(3)=9+6m+2m−1<0 ⇔ m²−2m+1>0 i 8m+8<0 ⇔ ⇔ (m−1)²>0 i m+1<0 ⇔ m≠1 i m<−1 ⇔ m<−1 ⇔ m∊(−∞;−1) . ...

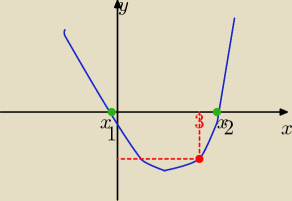
Eta: Można też tak : Parametr "m" musi spełniać układ warunków 1^o Δ>0 2^o f(3) <0 ad1^o jak podała Basia Δ>0 m€R\{1} ad2^o f(3)= 9+6m+2m −1 <0⇒ 8m < −8 ⇒ m<−1 odp: dla m < −1

Eta: Echh pigor ( zeszło mi, bo rysowałam