Mrówka: Stożek przecięto płaszczyzną równoległą do podstawy w połowie wysokości. Ile razy objętość dolnej części jest większa od górnej?

pigor: ... otóż z warunków zadania i tw. o stosunku objętości figur podobnych przy ... domyślnych oznaczeniach :

	Vg
Vg+Vd=V i		=(12)3=18 ⇒ V=8Vg i Vg+Vd=8Vg ⇒
	V

⇒ V_d=7V_g , czyli 7 razy V dolnej (d) części większa od V górnej (g) . ...

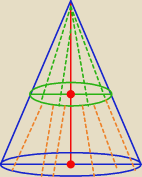Eta: Stożek duży ( niebieski) jest podobny do stożka małego ( zielonego) w skali k=2 to:

	VD
		= k3= 8
	Vm

	1
Vm=		VD to V (ścięty ) (brązowy) ma objętość 7 razy większą od V małego
	8

Beti:

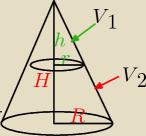
	1
h =		H
	2

	h		H
z tw. Talesa:		=
	r		R

	h*R
r =
	H

	1   H*R 2
r =
	H

	1
r =		R
	2

	1
VS =		πR2H
	3

	1		1		1		1		1
V1 =		πr2h =		π*		R2*		H =		πR2H
	3		3		4		2		24

	23
V2 = VS − V1 =		πR2H
	24

	V2		23   πR2H 24		23		24
więc:		=		=		*		= 23
	V1		1   πR2H 24		24		1

czyli dolna część ma objętość 23 razy większą od górnej części

Eta: ?

Beti: no tak... błąd w obl. V₂

	7
V2 = VS − V1 =		πR2H
	24

	V2		7		24
więc		=		*		= 7
	V1		24		1

i się zgadza...

Eta: