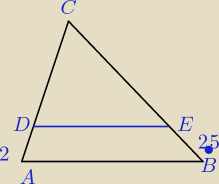
PLANIMETRIA mahrek: Trójkąty ABC i DEC są podobne. Obwód ABC jest o 6 wiekszy od obwodu DEC.: Oblicz: a) dlugoscb odcinka EC b)obwody ABC i DEC Próbuję to rozwiazac ale wychodza mi sprzecznosci...a.5

Basia: a co to jest 2 i 2,5 ? AD = 2 i BE = 2,5 ? czy coś innego ?

mahrek: tak...

Basia: no to też mi sprzeczność wyszła

mahrek: w odp jest ze EC=7.5 obw 24 i 18...nie AB−DE=1,5 AB+BC+AC=CD+CE+DE+6 jezeli przeniose AB na druga to z tej roznicy mam 1.5 BC+AC=CD+CE+7.5 CD+2+CE+2.5=CD+CE+7.5 co jest sprzeczne nie?

Basia: tu popełniasz błąd DE − AB = [c[−]1,5 i tu akurat nie ma sprzeczności może gdzieś się pomyliłam; policzę jeszcze raz

mahrek: i jak?

Basia: chyba czegoś nie doczytałeś w tym zadaniu takich trójkątów jest nieskończenie wiele; pasuje każda para o bokach: DC=2a; EC=2,5a; DE=1,5a i AC=2a+2; BC=2,5a+2,5; AB=1,5a+1,5 gdzie a jest dowolną liczbą R₊ może skala podobieństwa jest podana albo długość jeszcze któregoś odcinka do odpowiedzi z książki: a=3 ale dla każdego innego a>0 też będzie dobra odpowiedź czyli musiałeś coś przegapić

mahrek: wlasnie nie...tak jest napisane dokladnie jakpodalem powyzej: tylko ze jest jeszcze AB||DE

Basia: no to, jak widać, zadanie jest źle sformułowane mogę Ci najwyżej wyjaśnić jak doszłam do tego co napisałam wyżej

mahrek: nie nie trzeba

Michał: Basia 2 podpowiedzi: Po 1 używając samej algebry pomijamy fakt podobieństwa trójkątów, który pozwala nam wykorzystać w układach równań m.in twierdzenie cosinusów na kącie ACB zarówno dla wiekszego, jak i mniejszego trójkąta (dodając 2 równania i jedną niewiadomą), co sprawi, że bedzie tylko 1 wynik. Z ciekawostek, można rozwiązac to stosując twoje równanie poszerzone o twierdzenie Talesa i podobieństwa trójkątów; (stosunki proporcji)