Mrówka: udowodnij że suma odległości dowolnego punktu M, leżącego wewnątrz trójkąta równobocznego ABC, od boków tego trójkąta jest stała i równa się wysokości tego trójkąta

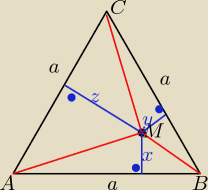
Basia: P_ABC = P_AMB+P_BMC+P_AMC P_AMB = ¹₂a*x P_BMC = ¹₂a*y P_AMC = ¹₂a*z P_ABC = ¹₂a*h podstaw do pierwszego równania i wylicz szukaną sumę x+y+z