Bardzo proszę o pomoc w rozwiązaniu zadań na zaliczenie semestru Synapse: Bardzo proszę o pomoc w rozwiązaniu zadań na zaliczenie semestru Oblicz równania i nierówności.

x − 2
	≥2
2x − 1

4x³ + 12x² − x − 3 < 0 x³ +x−2=0

ewa: 3) x³−x²+x²−x+2x−2=0 x²(x−1)+x(x−1)+2(x−1)=0 (x−1)(x²+x+2)=0 x=1 ( w drugim nawiasie nie ma pierwiastków bo Δ=1−8<0 ) Zatem x=1 jedyne rozwiązanie

ewa:

	x−2		1
1)		−2≥0 zał. x≠
	2x−1		2

	x−2−4x+2
		≥0
	2x−1

	−3x
		≥0
	2x−1

	1		1
−6x(x−		)≥0 i x≠
	2		2

	1
x∊<0,		)
	2

Eta:

	1
1/ założenie 2x−1≠0 ⇒ x≠
	2

	x−2−2(2x−1)
		≥0
	2x−1

	−3x
		≥0
	2x−1

	1
x€ <0,		)
	2

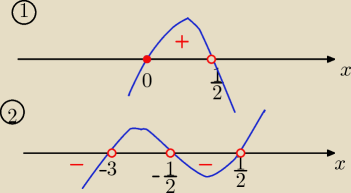
2/ 4x²(x+3)−(x+3) <0 (x+3)(4x²−1)<0 (x+3)(2x−1)(2x+1) <0

	1		1
x€ (−∞, −3) U ( −		,		)
	2		2

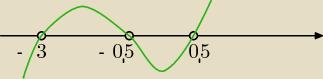
ewa: 2) 4x²(x+3)−(x+3)<0 (x+3)(4x²−1)<0

	1		1
4(x+3)(x−		)(x+		)<0
	2		2

x∊(−∞, −3)∪(−0.5 , 0.5)

Synapse: sory ale nie rozumiem 2 linijki w pierwszym przykładzie jakim cudem jest w liczniku x−2−4x+2

Synapse: sory ale nie rozumiem 2 linijki w pierwszym przykładzie jakim cudem jest w liczniku x−2−4x+2

Synapse: sory ale nie rozumiem 2 linijki w pierwszym przykładzie jakim cudem jest w liczniku x−2−4x+2

%25253Cb%25253ESynapse%25253A%25253C%25252Fb%25253E%252520sory%252520ale%252520nie%252520rozumiem%2525202%252520linijki%252520w%252520pierwszym%252520przyk%2525C5%252582adzie%252520jakim%252520cudem%252520jest%252520w%252520liczniku%252520x%2525E2%252588%2525922%2525E2%252588%2525924x%25252B2%25253Cimg%252520style%25253D%252522margin-bottom%25253A-3px%252522%252520src%25253D%252522emots%25252F2%25252Fpytajnik.gif%252522%25253E%25250A%25250A

Eta: x−2−2*(2x−1) = po wymnożeniu ....= x−2 −4x+2

ewa: Sprowadzamy do wspólnego mianownika:

x−2		2(2x−1)
	−		≥0
2x−1		2x−1

Synapse: sory że jestem taki tępy ale tego też nie kapuje −6x(−1/2)≥0 skąd to

ewa: Znak ilorazu jest taki sam jak iloczynu. Zamieniłam iloraz na iloczyn −3x*(2x−1) i wyciągnęłam

	1
2 z tego nawiasu, czyli −3x*2(x−		)≥0
	2

syanpse: (x+3)(4x²−1)<0 a to skąd

Artur_z_miasta_Neptuna: 4x²(x+3)−(x+3) = 4x²(x+3) + (−1)*(x+3) = // wyłącz część wspólną przed niawias // = = (x+3) * (4x² + (−1)) = (x+3)(4x²−1)

pigor: ... a ja proponuję ci trochę myśleć i "rozwalić toto" np. tak :

	x−2
1)		≥2 /*(2x−12 i 2x−1≠0 ⇔ (x−2)(2x−1)≥2(2x−1)2 i 2x≠1 ⇔
	2x−1

⇔ (x−2)(2x−1)−2(2x−1)²≥0 i (*) x≠¹₂ ⇒ (2x−1)(x−2−4x+2)≥0 ⇔ ⇔ 2(x−¹₂)(−3x)≥0 ⇔ −6x (x−¹₂)≥0 ⇒ stąd i z (*) 0≤x<¹₂ , czyli x∊<0;¹₂) − szukany zbiór rozwiązań danej nierówności ; −−−−−−−−−−−−−−−−−−−−−−−−− 2) 4x³+12x²−x−3<0 ⇔ 4x²(x+3)−1(x+3)<0 ⇔ (x+3)(4x²−1)<0 ⇔ ⇔ 4(x+3)(x−¹₄)<0 ⇔ 4(x+3)(x−¹₂)(x+¹₂)<0 ⇔ x<−3 ∨ (−¹₂<x<¹₂) ⇔ ⇔ x∊(−∞;−3)U(−¹₂;¹₂) − szukany zbiór rozwiązań ; −−−−−−−−−−−−−−−−−−−−−−−−−−−− 3) x³+x−2=0 ⇔ x³−1+x−1=0 ⇔ (x−1)(x²+x+1)+1(x−1)=0 ⇔ ⇔ (x−1)(x²+x+1+1)=0 ⇔ x−1=0 ∨ x²+x+2=0 ⇔ x=1 ∨ x∊∅, bo Δ=−7<0 ⇔ ⇔ x∊{1} − szukane rozwiązanie danego równania . ...

GRO: A nie może to być np tak : df= 2x−1≠0 2x≠1/:2 x≠ 1/2 x−2/2x−1≥2/*(2x−1) x−2≥2(2x−1) x≥4x x−4x≥0 −3x≥0/:(−3) x≤0 x∊<0;1/2) v 1/2∊\Df ?