ostrosłup Micha;: Długość wysokości ostrosłupa prawidłowego czworokątnego jest równa długości promienia okręgu opisanego na podstawie. Pole ściany bocznej tego ostrosłupa wynosi 18√3.

tim: Ok. Ja próbuję.

Micha;: ok

tim:

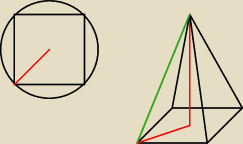
	1		1		a√2
r koła opisanego na podstawie =		d =		a√2 =
	2		2		2

	a√2
H =
	2

Więc tak.

	a√2
Zaznaczone na czerwono odcinki mają		.
	2

Korzystając z tw. Pitagorasa obliczamy bok zielony (krawędź boczna). <−− są też inne metody

	a√2		a√2
(		)2 + (		)2 = l2
	2		2

2a2		2a2
	+		= l2
4		4

a² = l² a = l Dalej. Widzimy, że wszystkie krawędzie ostrosłupa mają a. Pole ściany bocznej o wymiarach a, a, a = pole trójkąta równobocznego o boku a.

a2√3
	= 18√3
4

a² = 72 a = √72 Nie wiem co trzeba obliczyć

Micha;: objętość ostrosłupa ok Dzięki dalej dam sobie radę:

tim: Jeszcze poproszę Bogdana, Mickeja lub kogoś innego o sprawdzenie

Micha;: dobrze jest