Trygonometria...
Czarny jeż: Jest funkcja f(x)=cos2x − (1−sinx) . Trzeba znaleźć miejsca zerowe w przedziale <−π,π> i
rozwiązać nierówność f(x)>0 w tym samym przedziale.
Rozpisałałem sobie nieco tą funkcje . Ale nie wiem co dalej....
Mam tak:
f(x)= cos2x − sin2x −(sin2x + cos2x −sinx) = −2sin2x+ sinx
Co teraz ?
29 kwi 12:33
Bogdan:
Podpowiedź:
Podstawienie: t = sinx i t € <−1, 1>
29 kwi 12:40
Czarny jeż: No dobra . Wcześniej też na to wpadłem , ale nie wiedziałem co dalej... Ale teraz już to mam.
| | 1 | |
Nie wiem tylk jak z tą nierównością... mam , że t∊(0; |
| ) . I jak teraz to... nawet nie |
| | 2 | |
| | π | |
wiem jak nazwać to , co trzeba zrobić  Wynik wyszedł mi dobry, mianowicie (0; |
| )u |
| | 6 | |
| | 5π | |
( |
| ;π)... Ale nie wiem jak to zrobiłem 
|
| | 6 | |
Mógłbyś mi Bogdanie (albo ktokolwiek inny) wytłumaczyć krok po kroku jak powinienem rozwiązać
tą nierówność ? Z trygonometrii nigdy nie byłem zbyt cwany.
29 kwi 18:07
Czarny jeż: hop hop

29 kwi 20:02
29 kwi 20:06
Czarny jeż: I wartości mam odczytać poprostu z sinusoidy ?
29 kwi 20:14
Bogdan:
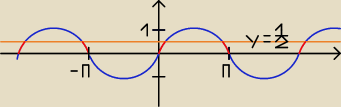
29 kwi 20:25
Bogdan:
Dla x € <−π, π>
sinx = 0 => x = 0 lub x = π
| | 1 | | π | | π | | π | | 5π | |
sinx = |
| => sinx = sin |
| => x = |
| lub x = π − |
| = |
| |
| | 2 | | 6 | | 6 | | 6 | | 6 | |
| | 1 | | π | | 5π | |
Dla sinx € (0, |
| ) x € (0, |
| ) U ( |
| , π) |
| | 2 | | 6 | | 6 | |
29 kwi 20:29
 Wynik wyszedł mi dobry, mianowicie (0;
Wynik wyszedł mi dobry, mianowicie (0;

