:) Jump: Oblicz pole trapezu o podstawach 2 i 11 oraz przekątnych 5 i 12

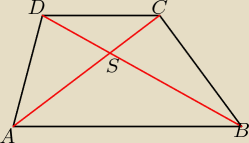
Basia: tr.ASB i tr.CSD są podobne

	AB		11
skala podobieństwa k =		=		= 5,5
	CD		2

stąd: AS = 5,5CS AS + CS = 5 5,5CS + CS = 5 6,5CS = 5

	50		10
CS =		=
	65		13

	10		55
AS = 5−		=
	13		13

analogicznie możesz policzyć BS i DS potem np.z tw.cosinusów w tr.ASB wyznaczysz cos(∡ASB) = cosα a sinα z jedynki trygonometrycznej

	1
P =		*[ AS*BS*sinα + CS*DS*sinα + AS*DS*sin(180−α) + BS*CS*sin(180−α) ]
	2

pigor: ... lub jak juz będziesz miał sin∡ASB , oblicz pole czworokąta (tu trapezu) ze wzoru P=¹₂|AC|*|BD|sin∡ASB = ¹₂*5*12*sin∡ASB = 30sin∡ASB = ...

Basia: oj pigor nic nie zostawiasz dla autora; przecież tam trzeba sin(180−α) zastąpić przez sinα i wyłączyć sprytnie przed nawias wyjdzie wzór, który podałeś

Izka: obliczyłam DS I BS wyniki to ²⁴₁₃ i ¹³²₁₃ ale nie umiem ruszyć tego dalej

Basia: teraz z tw.cosinusów masz AB² = AS²+BS² − 2AS*BS*cosα podstaw i wylicz cosα

Elka: wyszło mi że cosα=0

Izka: No mi też tak wyszło.

Elka: Izka widzę że nie tylko ja tu potrzebuje pomocy z planimetrii

Jump: a ja dalej nie czaje

Basia: niemożliwe; nie wychodzi cosα=0, ale rachunki są straszne (oczywiście na kalkulatorze da się policzyć) na pewno te podstawy to 2 i 11 ?

Jump: tak na 100%. W odpowiedziach mam że pole trapezu wynosi 30.

Basia: a to jednak dziewczęta dobrze policzyły ; to ja się pomyliłam cosα = 0 ⇒ α jest kątem prostym ⇒ sinα=1 ⇒ P = ¹₂*5*12*1 = 30 (patrz wzór pigora) a rozumieć nie ma co z tw.cosinusów masz AB² = AS²+BS²−2AS*BS*cosα 2AS*BS*cosα = AS²+BS²

	AS2+BS2−AB2
cosα =
	2AS*BS

to masz powyliczane; podstawiasz i liczysz

Jump: ok już kumam dzięki Basia wszystko rozumiem