. Ilona: Kto mógłby rozwiązać mi to zadanie i dokładnie wytłumaczyć? 5. W trapezie równoramiennym dana jest przekątna oraz kąty α i β, które ta przekatna tworzy odpowiednio z dłuzszą podstawą i ramieniem. Oblicz pole tego trapezu

Artur_z_miasta_Neptuna:

	h
sinα =		⇒ h = d*sinα
	d

a = b + 2y ⇔ a−y = b+y a+ b = 2b+2y ⇔ a+b = 2*(a−y)

	a−y
cos α =		⇔ (a−y) = d*cosα ⇔ a+b = 2*(a−y) = 2*d*cosα
	d

	(a+b)*h
Ptrapezu =		= .... podstaw ....
	2

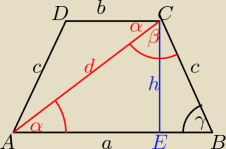Basia: γ = 180−(α+β) z tw.sinusów w tr. ABC wyliczysz a i c z definicji sinusa w tr.AEC wyliczysz h z definicji cosinusa (albo tangensa) w tr.BEC wyliczysz EB b = a−2EB no to już jest wszystko co potrzebne do policzenia pola