nierownosć olaaa: jest to chyba łatwe ale nic nie moge tu zauważyć musze rozwiazac pewna nierówność no i doszłam do takiego etapu (x−1)²(x+3)−(x−1)² > 0. i jak tu cos zredukowac? co dalej? bylabym bardzo wdzieczna za pomoc

czarny: nie wiem czy pomogę ale ja bym (x−1)² wyłączył przed nawias

olaaa: no no chybs o to chodzi, bo potem powstanie (x−1)²(x−2) >0 i sie zgadza wszytsko

Krzysiek: (x−1)²(x+3)>(x−1)² (x−1)² jest zawsze dodatnie wiec moge podzielić stronami przez (x−1)² x+3>1 x>−2 chyba

olaaa: dzieki bo ja niestety czesto tak mam ze jakies trudne rozwiazania widze od razu a te najprostsze umykaja

Krzysiek: a kto tak nie ma?

olaaa: (x−1)²(x+2) >0 i wtedy zaznaczamy na osi 1 i −2 i nam wychodzi x nalezacy (−2;1) suma (1, +niesk) i koniec

♊: jest pewna sprawa, o której Krzysiek nie wspomniał − niby oczywiste, ale zawsze (x−1)² nie jest ZAWSZE dodatnie. Dla x=1 wynosi 0. Więc trzeba będzie to uwzględnić w odpowiedzi (bo sprzecznością jest, że 0>0, a tak wychodzi dla x=1)

Krzysiek: Twoje rozwiązanie mnie dopiero uświadomiło, że jeszcze muszę dać założenie, że x−1≠0

olaaa: po to jest forum pomoc dziala w dwie strony pzdr

Bogdan: Nie wolno dzielić przez (x − 1)²,

♊: Bogdan: można, tylko trzeba sprawdzić, czy jakieś rozwiązanie nam przez to nie umknie. W tym zadaniu można podzielić przez (x−1)² bo żadnego rozwiązania się nie traci. Ja osobiście wyłączyłbym (x−1)² przed nawias i doprowadził do postaci (x−1)²(x+3−1)>0 iloczyn 2ch liczb jest większy od zera gdy obie liczby są tego samego znaku (czyli obie dodatnie lub obie ujemne). (x−1)² jest zawsze dodatnie, więc x+3−1 tez musi byc dodatnie w ten sposób otrzymujemy (x+3−1)>0 x>−2 czyli to co Krzysiek napisał w 29 kwi 11:07 Odpowiedź końcowa oczywiscie bez 1

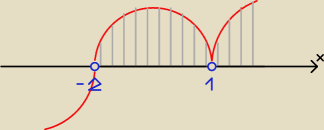
Bogdan: (x − 1)²(x + 3)−(x − 1)² > 0 (x − 1)²(x + 3 − 1) > 0 (x − 1)²(x + 2) > 0 rysunek x € (2, 1) U (1, +∞)

Bogdan: Ze względu na konieczność pilnowania, czy jakieś rozwiązanie nam nie umknie przy dzieleniu przez wyrażenie zawierające zmienną oraz ze względu na konieczność dokonania założenia przed wykonaniem dzielenia o tym, że wyrażenie ze zmienną ≠ 0, lepiej jest nie dzielić.